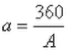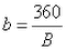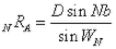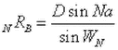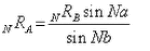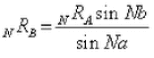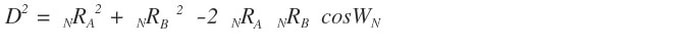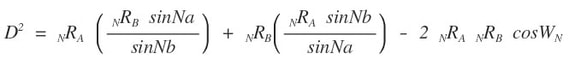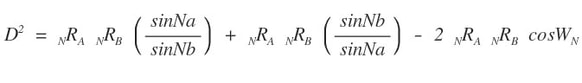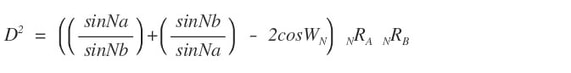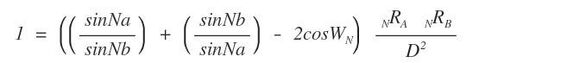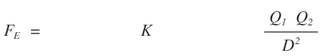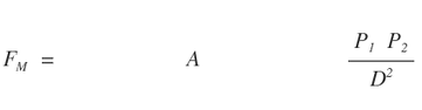Quantum Harmonic Bi-radial Field Streucture
Introduction
The origin of the bi-radial matrix
|
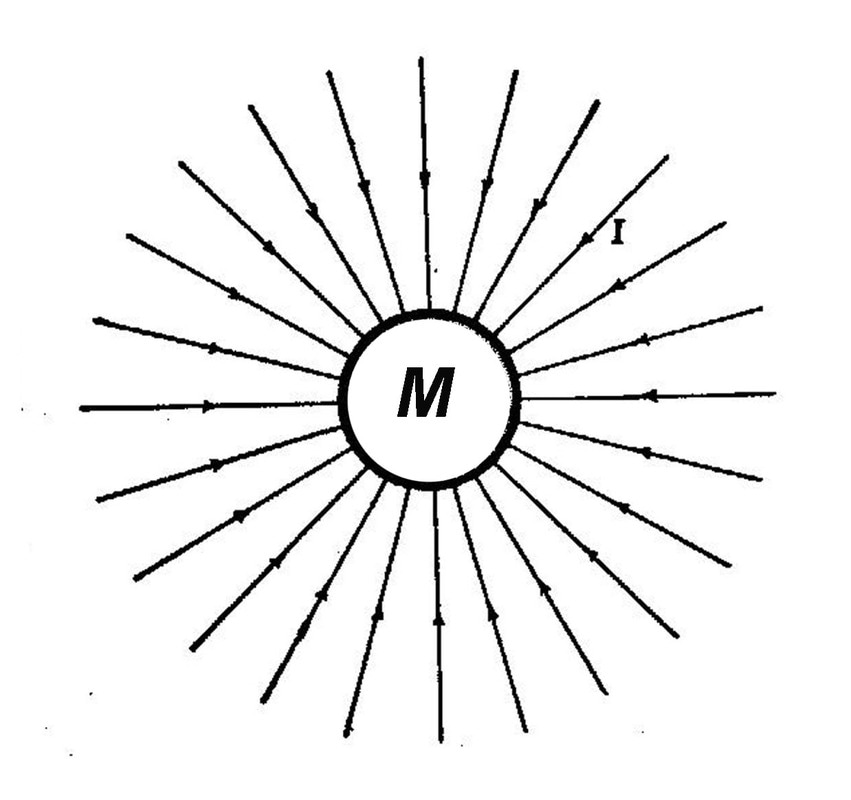
The bi-radial matrix started from a study of gravitation as illustrated in the following diagram. "A diagram of a gravitational field surrounding a spherical mass M of uniform density is shown in diagram 1. The arrows show the direction of the field as everywhere inward. The spacing of the lines shows the field is strongest at the surface. For every point at the same distance from the center, the field intensity I has the same magnitude."
Note: a spherical mass of uniform density does not exist in nature on a macroscopic scale. Thus this model can be considered an "ideal system". As the distance increases the field intensity decreases. As many radial lines as desired can be drawn to represent the field and they must be equally spaced. A greater number of rays corresponds to and is analogous to a greater mass and stronger gravitational field, and a smaller number of rays corresponds to a smaller mass and a weaker gravitational field. |
Diagram 1
|
|
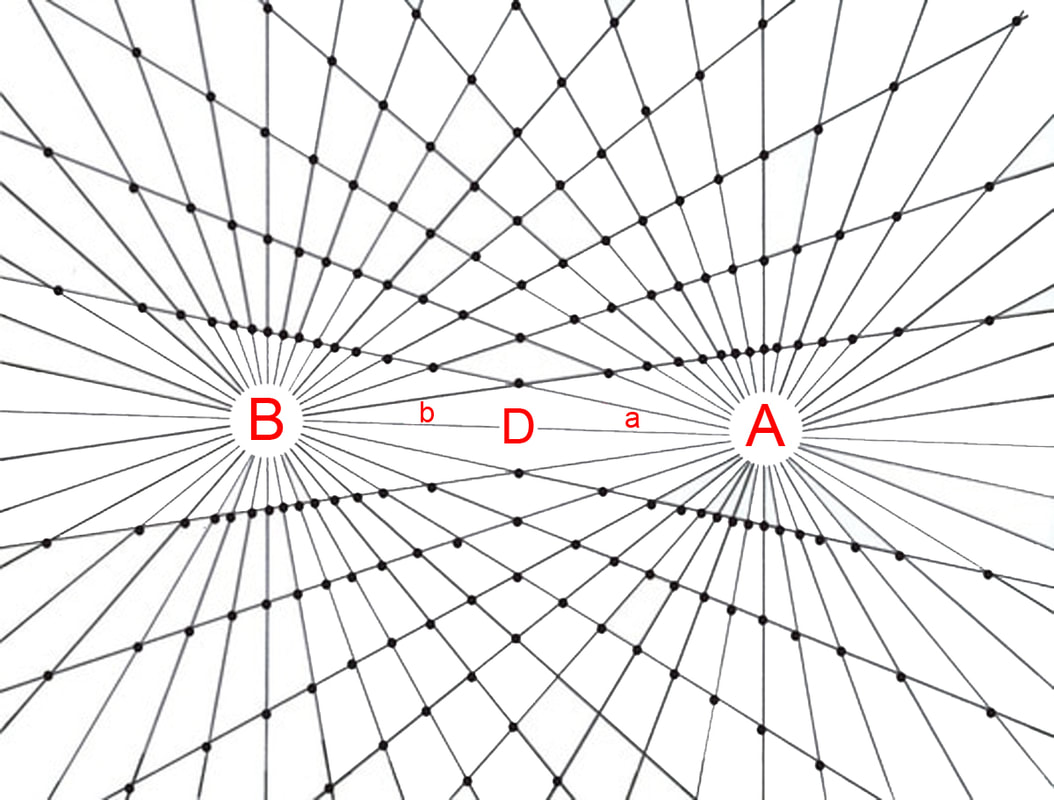
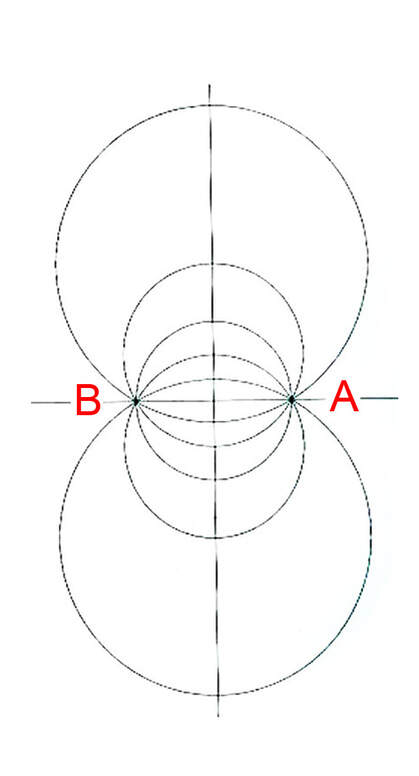
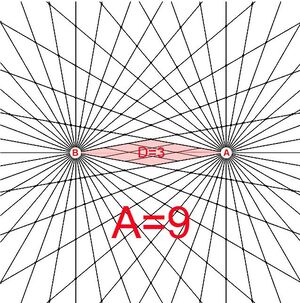
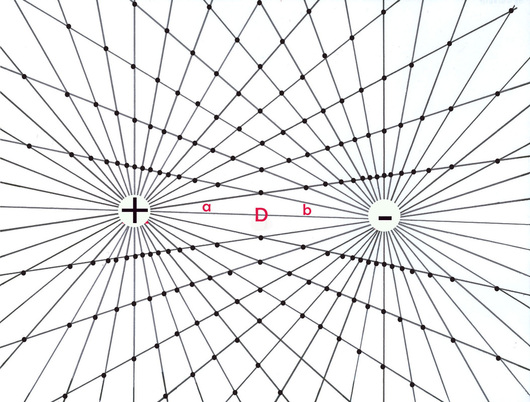
The bi-radial matrix began as an extension to this geometric analogy to represent two masses and their interacting gravitational fields as shown in diagram 2. The centers of the two "masses" generally designated as "poles" are indicated as "A and "B" separated by as distance "D". "A" also represents the number of rays from pole A and "B" represents the number of rays from pole "B". These represent the first three variables from which a detailed description of the bi-radial matrix is given.
|
Diagram 2
|
Upon further insight it turns out the bi-radial matrix represents something more fundamental than gravitation namely time and space. From the fundamental equation v=s/t it is known that space and time are two inseparable reciprocal aspects of motion. This is a fundamental relation in nature and the basis for an emerging theory called the Reciprocal system of Theories. Ironically this theory as originally presented by Dewey B. Larson lacked any detailed geometry to express the detailed force field structures of for instance electromagnetism and gravitation. We have corrected this and have developed a geometric expression of this fundamental space-time reciprocal relationship. As a member of ISUS from the mid1990's I collaborated with lead research scientist the late Bruce Peret in which I began the long process of correlating fundamental symmetries with the reciprocal space time relation. This included a presentation of my research at the 22nd Annual ISUS meeting held at L&L Research. This was an early step in the process before advanced computer programming was incorporated for the geometric modelling. A reprint of the original 1998 article in The Journal of Reciprocity (with detailed diagrams deleted) can be seen here: https://reciprocalsystem.org/papers-for-author/42
A detailed geometric analogy of time and space expressing this reciprocal relationship is pursued. Using geometric components to represent time and space fundamental force field structures are derived from first principles. In turn fundamental equations are derived from the structures. This includes a fundamental inverse square law and the harmonic series. This is an example of quantum reconstruction and it amounts to rebuilding quantum theory from scratch based on a few simple principles. This also applies to gravitation as it attempts to rebuild macrocosmic theories of gravitation from scratch from fundamental principles.
A detailed geometric analogy of time and space expressing this reciprocal relationship is pursued. Using geometric components to represent time and space fundamental force field structures are derived from first principles. In turn fundamental equations are derived from the structures. This includes a fundamental inverse square law and the harmonic series. This is an example of quantum reconstruction and it amounts to rebuilding quantum theory from scratch based on a few simple principles. This also applies to gravitation as it attempts to rebuild macrocosmic theories of gravitation from scratch from fundamental principles.
Background
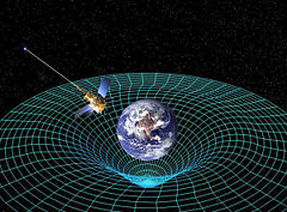Geometry of curved space-time
around a gravitational mass
Geometric structures are used to define fundamental physical phenomenon including the space time curvature of gravitational fields. The general inverse square law derived from an expanding sphere has wide spread application in physics. There is an increasing trend to pursue detailed, underlying and fundamental structures from which our physical laws will emerge as special cases. Some have in the case of the amplituhedron speculated that space and time are only a feature of the geometry. Our approach regards space and time as distinct entities albeit with geometric structure and a direct structural analogy to space and time is developed in pursuit of a commutative based quantum geometry.
In devising his own quantum geometry Roger Penrose puts it this way: "My own view is that ultimately physical laws should find their most natural expression in terms of essentially combinatorial principles, that is to say, in terms of finite processes such as counting or other basically simple manipulative procedures..."
In line with this approach logically extending an existing geometric model of gravitation reveals detailed force field structures from first principles emerging from combinations of equi-spaced radial lines and angles. The reciprocal relation between space and time is described in experiential terms. A geometric and numerical analogy of space and time consistent with this property is logically derived. The "basically simple" mathematical relations are derived directly from the primary structure and physical interpretations are pursued. This is facilitated by using a bi-radial coordinate system and is in pursuit of a fundamental structure or structures and resulting fundamental equations of which our known physics equations are special cases.
The bi-radial matrix is consistent with a background independent view of the universe. It is also consistent with time being primary and space being an emergent feature. Further research indicates a companion matrix which has the inverse properties. A broader aim of this research is to combine these two matrices with other similar matrices for a comprehensive integrated description of the space-time plenum in terms of finite processes, basically simple manipulative procedures and geometric structure.
In devising his own quantum geometry Roger Penrose puts it this way: "My own view is that ultimately physical laws should find their most natural expression in terms of essentially combinatorial principles, that is to say, in terms of finite processes such as counting or other basically simple manipulative procedures..."
In line with this approach logically extending an existing geometric model of gravitation reveals detailed force field structures from first principles emerging from combinations of equi-spaced radial lines and angles. The reciprocal relation between space and time is described in experiential terms. A geometric and numerical analogy of space and time consistent with this property is logically derived. The "basically simple" mathematical relations are derived directly from the primary structure and physical interpretations are pursued. This is facilitated by using a bi-radial coordinate system and is in pursuit of a fundamental structure or structures and resulting fundamental equations of which our known physics equations are special cases.
The bi-radial matrix is consistent with a background independent view of the universe. It is also consistent with time being primary and space being an emergent feature. Further research indicates a companion matrix which has the inverse properties. A broader aim of this research is to combine these two matrices with other similar matrices for a comprehensive integrated description of the space-time plenum in terms of finite processes, basically simple manipulative procedures and geometric structure.
Bi-Concentric Matrix
Key points to be covered in detail
1) Defining space and time in geometric terms as two reciprocal aspects of motion
2) Deriving a scaling mechanism invariant under spatial transformation and a range formula- the key to unification
3) Developing a bi-radial harmonic coordinate system revealing the underlying information matrix
4) Developing a bi-polar/bi-radial quantum geometry
5) Deriving fundamental force field structures (lines of force) from an underlying matrix
6) Identifying the harmonic relation between space and time
7) Deriving an alternative bi-radial inverse square relations over distance from first principles
8) Showing the fundamental forces aka force fields in nature are holographic interference patterns
9) Pursuing testable hypotheses regarding magnetic and gravitational field structures
10) Comparing bi-radial matrix to existing theories, models and concepts
PART 1
Section 1 Reviewing existing model of Gravitation
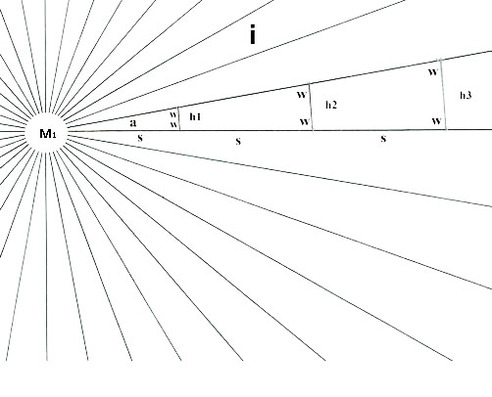Diagram 1
Diagram 1 depicts a gravitational field around a spherical mass M1 with uniform density. There can be as many or few lines as desired and they must be equi-spaced. As one researcher puts it: "The lines themselves are imaginary and do not actually exist; they are introduced as an aid to the understanding of gravitational forces and gravitational phenomenon." See part 3 sections 3-7. For every location at the same distance from the center the field intensity i has the same magnitude.
This model partially agrees with observation. As objects fall they converge towards a common center of gravity. The spacing of the lines shows the field is strongest at the surface. In this analogy the greater number of equi-spaced lines corresponds to a greater mass and stronger gravitational field. Is there a way to extend this analogy to describe an inverse square relation between TWO masses and two interacting gravitational fields as described in Newton's law of gravitation?
This model partially agrees with observation. As objects fall they converge towards a common center of gravity. The spacing of the lines shows the field is strongest at the surface. In this analogy the greater number of equi-spaced lines corresponds to a greater mass and stronger gravitational field. Is there a way to extend this analogy to describe an inverse square relation between TWO masses and two interacting gravitational fields as described in Newton's law of gravitation?
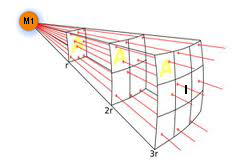Diagram 1A
Note: The geometric analogy of a single gravitational field around a given mass such as the earth as well as any single point source which spreads its influence equally in all directions is explained using the surface of a sphere where the area of the spherical surface changes per the square of the radius. The field intensity I at any given radius r is the source strength divided by the area of the sphere. Note in this model the areas depicted are not physical quantities. It is only with physical interpretation that "force" and the quantity I is associated with this model. This inverse square being strictly geometrical applies to diverse phenomenon including point sources of light, radiation, sound and electric fields.
The BRM is similar only it applies to interacting fields from two point sources or bi-polar fields including magnetic fields and two interacting gravitational fields. See part 9, Section 13 on Newton's Superb Theorem.
The BRM is similar only it applies to interacting fields from two point sources or bi-polar fields including magnetic fields and two interacting gravitational fields. See part 9, Section 13 on Newton's Superb Theorem.
PART 2 Developing a quantum geometry
Section 1A Extending the geometric analogy to gravitation
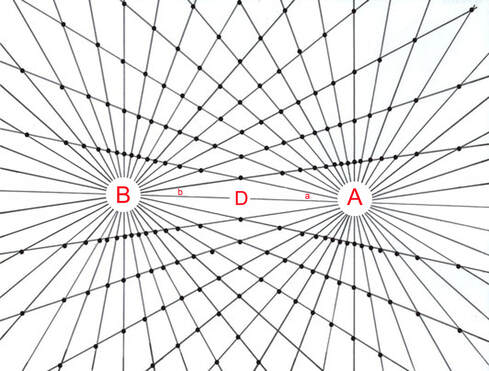
Diagram 2 Two Masses 'A' and 'B' with interacting gravitational fields
Two "masses" A and B separated by a distance D who's gravitational field interact forming nodes at the intersection of the rays.
Section 1B Initial variables
A = number of equi-spaced rays from pole A
B = number of equi-spaced rays from pole B
a = associated angles around pole A
b = associated angles around pole B
D = distance between pole A and pole B
I2 = field intensity within interaction region between two gravitational fields
Before developing the quantitative relations qualitative properties of the geometrical structure are shown and a review of space time graphs and a bi-radial coordinate system is derived from first principles.
Section 2 The Geometric properties of the Bi-Radial Matrix
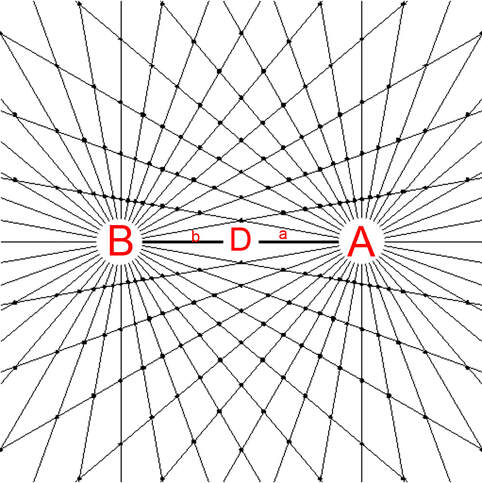
Diagram 3
Observe the trapezoids in diagrams 2 , 3 and 5 and the diamond shaped central region in each diagram. As the distance "D" between poles "A" and "B" decrease or increase the shapes of all the trapezoids and the diamond shape remain the same; i.e. the same internal angles, the same proportion in relation to surrounding trapezoids. This property of the BRM is "scale invariant" i.e. invariant under spatial transformation and will be explored further. It is easy from the initial variables to calculate all the interior angles of the trapezoids and show that all of them, per the principle of congruence remain the same shape regardless of the value of "D". From this we can prove the bi-radial matrix is scale invariant. See part 9, section 12 for comparison with conformal field theories. The trapezoid formulas are in the "Equations and Proofs" drop down menu of this web site. Review bi-radial coordinate system first. As gravitational fields relate to the geometry of space time a brief review of space time graphs is given.
Section 3 Plotting and graphing space and time.
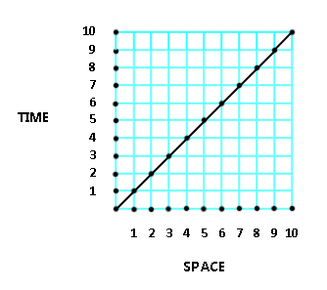Diagram 4A
Graphs such as that shown in diagram 4A are used to plot space-time relationships such as linear motion and acceleration. They are typically rectilinear Cartesian x-y axis oriented. In graphs like this linear motion results in a straight line graph where each segment represents a unit of space-time. It is revealing to use radial graphs to plot space time relationships. To show how the bi-radial matrix can be used to plot and graph space time relationships it is useful to develop a bi-radial coordinate system. First a brief survey a of polar coordinate system for graphing space time.
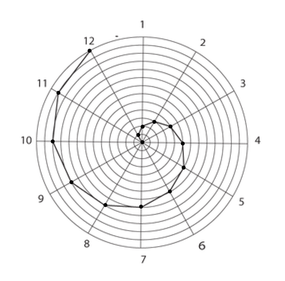Diagram 4B
Using a polar coordinate system where each ray marks the end of a unit time and the distance between the concentric circles represent unit space the graph of linear motion falls along the path of a spiral. Each segment along the spiral represents a unit of space-time. A bi-polar coordinate system can be used to plot space time. See part 3 section 3.
Section 4 Revealing nature's bi-Radial coordinate system
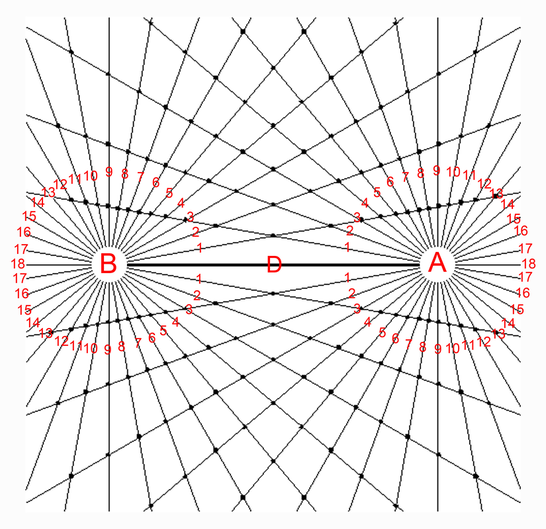
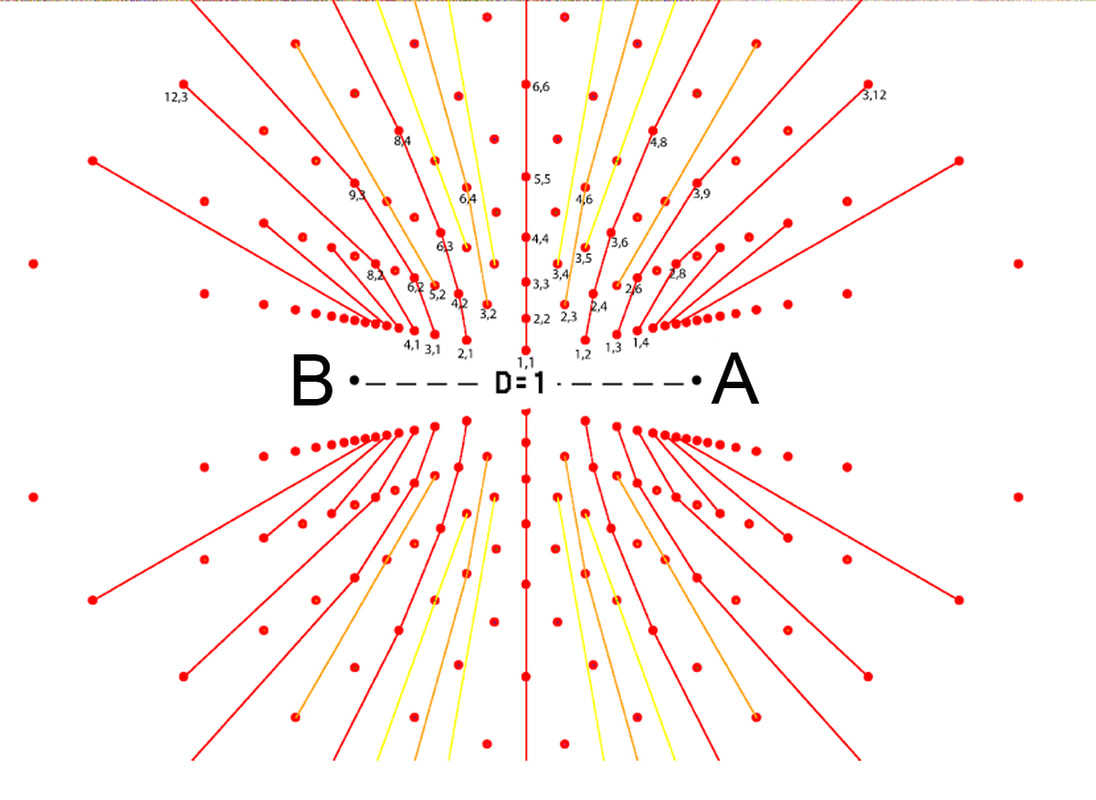
Diagram 5 Both opposing sets of rays are numbered in opposite directions.
From diagram 2 as the two centers are opposite each other it is logical and revealing to number the sets of rays from each "pole" in opposite directions starting from the "D" segment. The geometry of the matrix is based on the phenomenon of angular displacement by discrete intervals. Where do we routinely observe and employ angular displacement indicated by discrete intervals?
Section 5 Geometric definition of time
Time! Physics has recognized two forms of time : 1) Absolute time and 2) Clock time. Clock time may be regarded as "relative time". Clock time has for millennium been revealed and regarded as angular displacement indicated by discrete or quantized angular intervals since the advent of sun dials. Sun dials are based on rotational and orbital components of the Earth Sun system. This involves two reference systems.* The BRM reflects this. Without two reference systems pole A is only a time potential. Time is relational. Upon the presence of a second time frame or potential, pole "B" the "space" between them, the "D" segment and the spatial sub-divisions along the rays defined by the nodes occurs. This precisely models the scenario where time is fundamental and space is emergent.
Time is still regarded as angular displacement defined by discrete intervals.The space-time relationship is clarified arriving at working definitions of space and time. After the bi-radial coordinate system is described space and time are graphed with the BRM similar to diagrams 4A and 4B. See section 3 part 3. Every 360 degrees of the Earth's rotation around it's axis is tantamount to saying 24 hours has elapsed. Hence every 15 degrees of the earth's rotation is tantamount to saying 1 hour has elapsed. Every 360 degrees of the Earths orbital displacement around the sun in tantamount to saying one year has elapsed. Time IS quantized angular displacement in any direction.
The following table clarifies the quantized rotational nature of time.
1 second x 60 = 1 minute = 60 seconds = .25º rotation of Earth around its axis
1 minute x 60 = 1 hour = 3600 seconds = 15º rotation of Earth around its axis
1 hour x 24 = 1 day = 86400 seconds = 360º rotation of Earth around its axis
1 day x 7 = 1 week = 604800 seconds = 2520º rotation of Earth around its axis
1 week x 52= 1 year = 31449600 seconds = 131040º rotation of Earth around its axis
= 360º rotation of Earth around Sun
1 minute x 60 = 1 hour = 3600 seconds = 15º rotation of Earth around its axis
1 hour x 24 = 1 day = 86400 seconds = 360º rotation of Earth around its axis
1 day x 7 = 1 week = 604800 seconds = 2520º rotation of Earth around its axis
1 week x 52= 1 year = 31449600 seconds = 131040º rotation of Earth around its axis
= 360º rotation of Earth around Sun
Geometric definition of Time and Space
A general definition of space (s) and time (t) is implied in the definition of motion. The simplest form for an equation describing motion as defined for scientific and engineering purposes is v=s/t. This indicates that space and time are two reciprocal aspects of that motion and nothing else. If train A travels twice as fast as train B it makes no difference if we say train A twice as far in the same time as train B or that it travels the same distance in half the time as train B. 2s/1t=1s/(1/2t) This reciprocal relation between space and time has a numerical-mathematical and geometric expression using equi-spaced rays and angles. See part 9, sections 1-3. Are there precise geometric definitions of time and space which are consistent with this reciprocal properties ?
General definitions of space and time
Time: discrete angular displacement in any direction.
The variable "a" in section 7 diagram 7 below represents a "moment" or "quanta" of time the result of dividing the 360 degrees around pole A by any counting number. The variable "b" represents a moment or quanta of time the result of dividing the 360 degrees around pole B by any counting number. Note a quanta of time is a discrete unit of time. A "quantum" of time would be the shortest possible duration of time whose value has yet to be determined.
Space: discrete linear displacement in any direction See section 9 diagram 30.
The variable "a" in section 7 diagram 7 below represents a "moment" or "quanta" of time the result of dividing the 360 degrees around pole A by any counting number. The variable "b" represents a moment or quanta of time the result of dividing the 360 degrees around pole B by any counting number. Note a quanta of time is a discrete unit of time. A "quantum" of time would be the shortest possible duration of time whose value has yet to be determined.
Space: discrete linear displacement in any direction See section 9 diagram 30.
Both space and time are forms of displacement, one linear, the other angular. Space is progressive, (clock) time is cyclical. These definitions are corollaries of two fundamental postulates forming the basis of a comprehensive physical theory. See part 9 section 5. In diagram 5 each pole represents a separate time frame numbered in opposite directions per their opposing orientation and to allow for opposite time flow. Each number and corresponding ray marks the end of one discrete moment of time and the beginning of another like on clock faces. See Part 3, section 3. There is the primary space separating poles "A" and "B", the D segment and the spatial subdivisions along the rays defined by the nodes. Notice that the time intervals are unitized and the spatial intervals are non-unitized; integer vs real. This is a result of the reciprocal relation between space and time.
Section 6 The intersection nodes from the two sets of rays
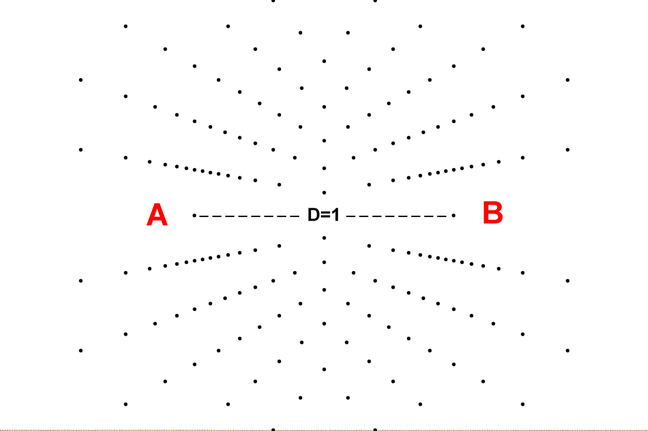Diagram 6
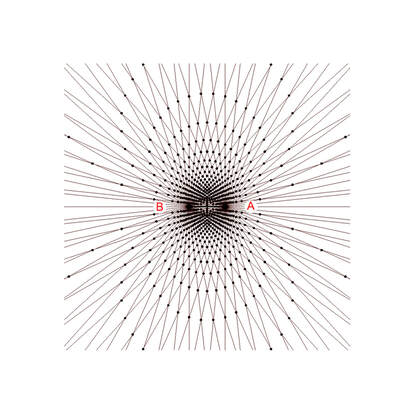
Diagram 6 shows the intersection nodes from the two sets of equi-spaced rays from diagram 5.This is an interference pattern. Notice the non-uniform spacing between the nodes. The vertices are assigned coordinates based on the ray numbers assigned to the rays which create them. See diagram 7.
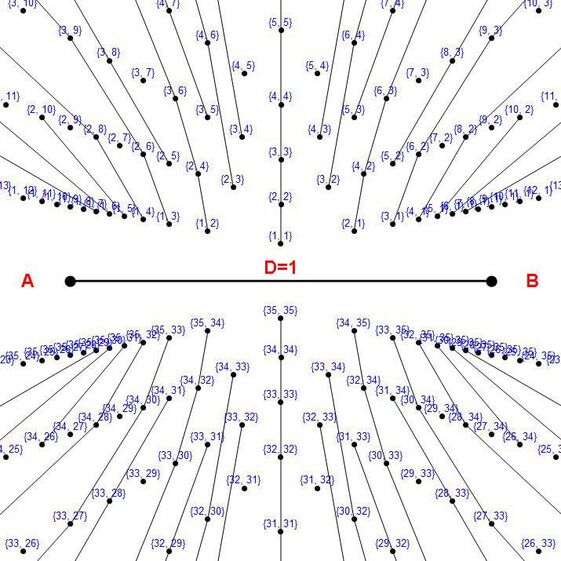
Section 7 Assigning the nodes bi-radial coordinates
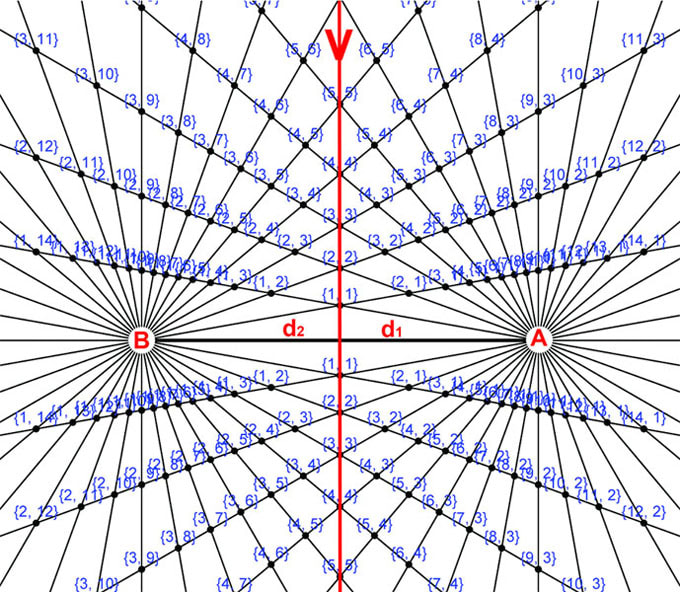Diagram 7
Diagram 7 assigns bi-radial coordinates to the intersection nodes resulting from the interference pattern. Owing to the dense population of the nodes in certain regions not all the corresponding coordinates are legible. The coordinates are designated as (x,y) where x refers to the ray number from pole A and y refers to the ray number from pole B. All nodes in any bi-radial matrix have coordinates except the A and B poles. Also recall from diagram 5a that if the pie sections were numbered instead of the lines between them the trapezoids would become the "coordinates".
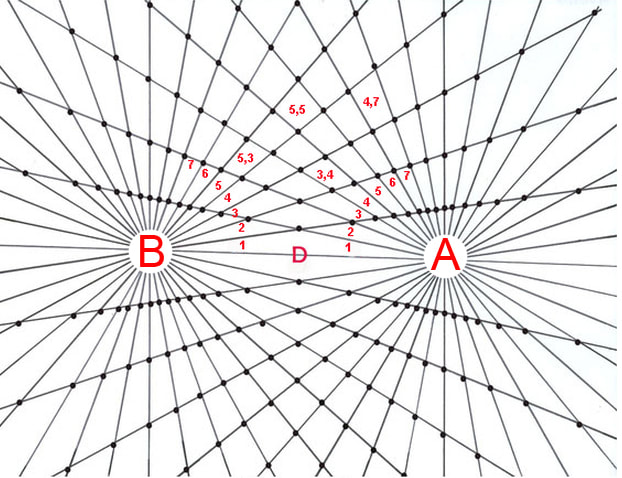Diagram 7A
Note some times it is convenient to number the pie sections as they represent the discrete moments of time them selves as opposed to the imaginary lines separating them. In this case the trapezoids become the "coordinates" in the BRM. Diagram 7a shows a sample of the angular sections numbered and a random sample of the trapezoids with their resulting coordinate pairings.
PART 3 Modeling of Gravitational and Electromagnetic Fields
Section 1 Bi-radial "attraction lines" and connection algorithm.
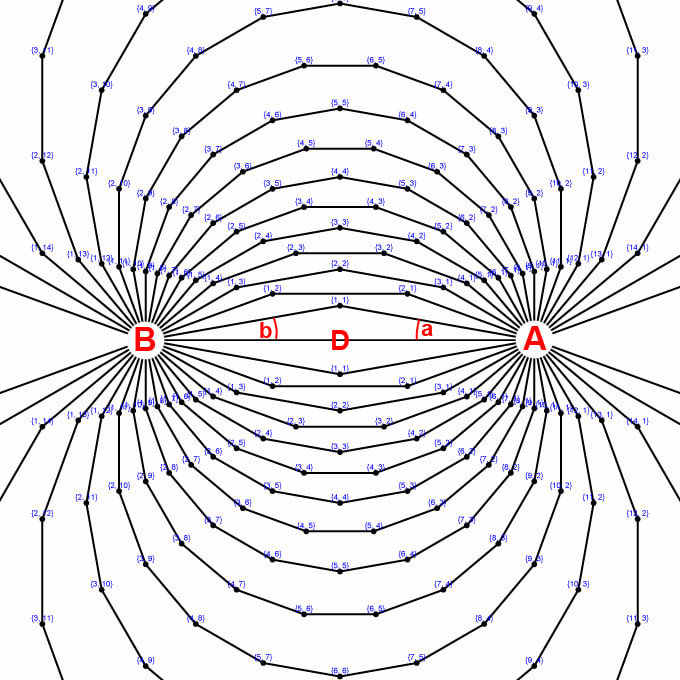Diagram 8
There are two primary algorithms by which to connect the nodes. Starting from the D segment and working outwards the shortest available path from "A" to "B" passing through unoccupied nodes. For example: A, (1,1), B (in the upper and lower hemispheres) are the two shortest paths from A to B passing through unoccupied nodes. These form the inner diamond shape.The next two shortest paths from A to B passing through the unoccupied nodes are: A, (2,1), (1,2), B in the upper and lower hemisphere. Using this algorithm of "shortest distance between A and B through unoccupied nodes" to define the paths until all the nodes are occupied forms a familiar pattern. This is comparable to the attraction "lines of force" around a magnet as shown in diagram 9.
The shortest distance of these linear paths is similar to electricity which travels along the path of least resistance which is often the shortest distance.* The aggregate of these curved lines are analogous to magnetism. These attraction lines fall along the paths of non-concentric circles whose diameters and centers have been formulated from the matrix. See section 2 in the equations and proofs drop down menu. These lines of force are a cross section of a toroidal field. By rotating the diagram 8 360 degrees around the D axis with a constant sampling rate a symmetrical torus is formed. This represents a larger 3-D aggregate of field lines which provides more information on modeling gravitational fields.* We will introduce 3-D modelling ahead to derive a torous (yin) and the counter torous (yang).
The bi-radial matrix represents an "ideal" condition giving rise to perfect symmetry. Actual magnets may have non-uniform density and other irregularities giving rise to slightly irregular field structure. In reference to gravitation the BRM represents two perfectly spherical masses with perfectly uniform density and (in the special case where A=B) of the exact same mass. This is not observed on the macroscopic scale. The bi-radial matrix is an ideal prototypical model indicating ideal conditions.
The shortest distance of these linear paths is similar to electricity which travels along the path of least resistance which is often the shortest distance.* The aggregate of these curved lines are analogous to magnetism. These attraction lines fall along the paths of non-concentric circles whose diameters and centers have been formulated from the matrix. See section 2 in the equations and proofs drop down menu. These lines of force are a cross section of a toroidal field. By rotating the diagram 8 360 degrees around the D axis with a constant sampling rate a symmetrical torus is formed. This represents a larger 3-D aggregate of field lines which provides more information on modeling gravitational fields.* We will introduce 3-D modelling ahead to derive a torous (yin) and the counter torous (yang).
The bi-radial matrix represents an "ideal" condition giving rise to perfect symmetry. Actual magnets may have non-uniform density and other irregularities giving rise to slightly irregular field structure. In reference to gravitation the BRM represents two perfectly spherical masses with perfectly uniform density and (in the special case where A=B) of the exact same mass. This is not observed on the macroscopic scale. The bi-radial matrix is an ideal prototypical model indicating ideal conditions.
Bi-Radial Structure of Magnetic Field.
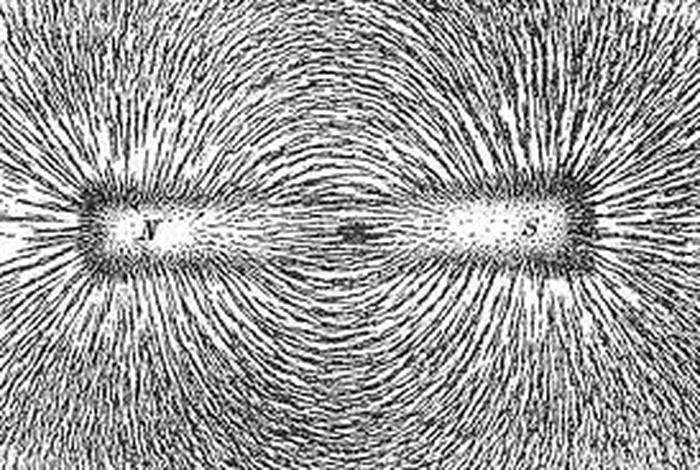
Diagram 9 Magnetic attraction lines of force as revealed with iron filings
These are traces of magnetic attraction lines of force such as those observed by Faraday. From the results of the present investigation we can hypothesis that their underlying structure is bi-radial.
Superimposing bi-radial attraction lines with actual magnetic attraction lines
Diagram 10
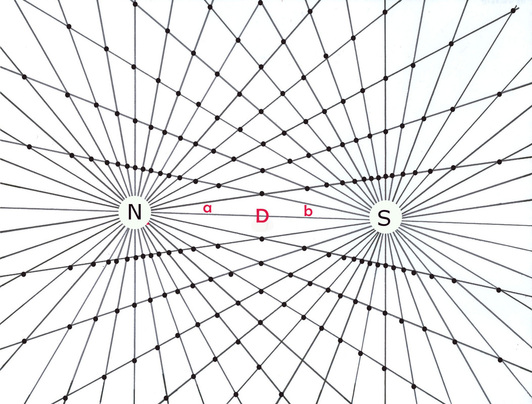
Diagram 10 highlights the bi-radial attraction lines from diagram 8 in red and superimposes them over traces of actual magnetic attraction lines with the same distance between the poles A,B and N,S. There is a structural similarity in both patterns. Are there mathematical similarities between the two patterns? This will be explored shortly.
Section 2 Analyzing structure of attraction lines
Secondary non-concentric circular sub-structure
 Diagram 11A
The end points of the segments (the nodes) which form the attraction lines in the BRM fall along the paths of non-concentric circles.The centers of these circles can be calculated based on the parameters in the matrix, See the "equations and proofs" drop down menu on this site.
|
 Diagram 11B
A change in distance D between the poles changes the scale of the non-concentric circles, not their relative proportions. A proportionate change in the ray numbers from each pole without a change in distance between the poles does not change the location or diameter of the circles, only the sampling rate within the BRM. See "Shell theorem" in Equations and proofs drop down menu for details. |
Section 3 Plotting space and time in the bi-radial matrix
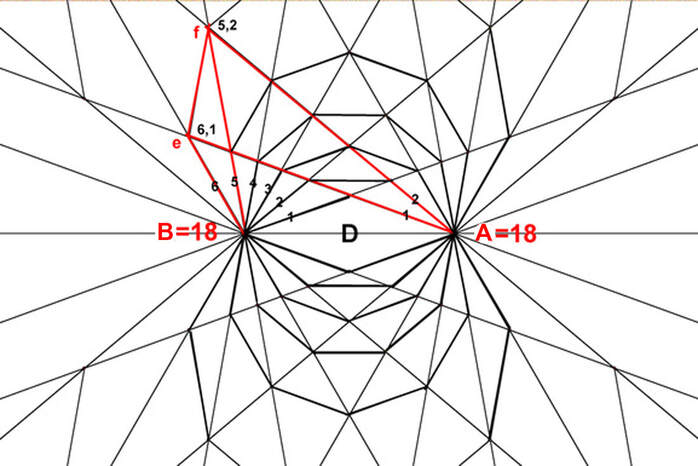Diagram 12
Continuing from diagrams 4a and 4b diagram 12 shows the space-time graph of the attraction lines where each ray marks the end of one moment of time and the beginning of the next. For example see segment ef. In relation to pole A it starts at the end of the first segment along ray 6 (6,1) and ends at the end of the second segment along ray 5, (5,2) . In relation to pole B it starts at the end of the 6th segment along ray 1 and ends at the end of the 5th segment along ray 2. In both reference frames segment ef represents a unit of space-time, only it's a different unit of space and time for each reference frame. Relative to pole A the segment ef represents outward motion in "reverse" time from moment 6 to moment 5. Relative to pole B segment ef represents outward motion in "forward" time from moment 1 to moment 2. This applies to all attraction segments and shows how this field structure is directly expressed in terms of space and time. Notice that neither space or time are curved, rather the paths of the attraction lines fall along curved paths (of circles). A similar graph for the repulsion lines indicates they can also be expressed directly in terms of space and time. (Not shown).
Section 4 Geometric derivation of repulsion lines
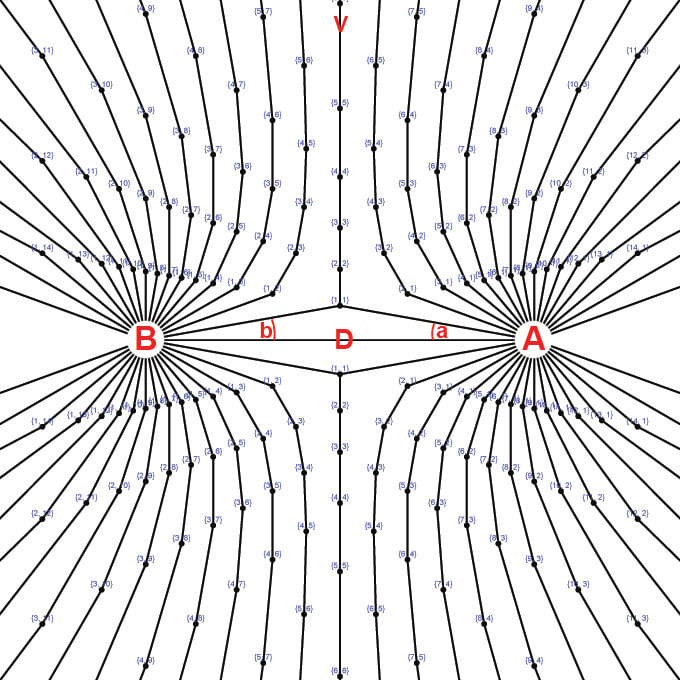Diagram 13
The second primary connection mode is shown in diagram 13. The algorithm to determine the paths of the repulsion lines relates to the shortest distance only it refers to the vertical "V" axis which bisects the D segment. Starting from the poles A and B the paths through the unoccupied nodes which either include the vertical axis or are otherwise the shortest distance from the vertical (V) axis passing through the unoccupied nodes make up the repulsion lines. The resulting "repulsion field" is superimposed with the coordinates of the Bi-Radial Matrix. These are analogous to the "repulsion lines of force" between two like poles of opposing magnets as shown in diagram 14. Both these repulsion lines of force and the attraction lines of force in diagrams 9 have simple mathematical expressions within the bi-radial coordinate system. The BRM shows that the orientation of the repulsion lines are about the V axis which in the special case of the BRM (when A=B) is perpendicular with respect to attraction lines who's symmetry is about the D axis. The bi-radial equations for the attraction and repulsion lines are shown in part 4, section 1.
"Repulsion lines of force" between two like poles of opposing magnets.
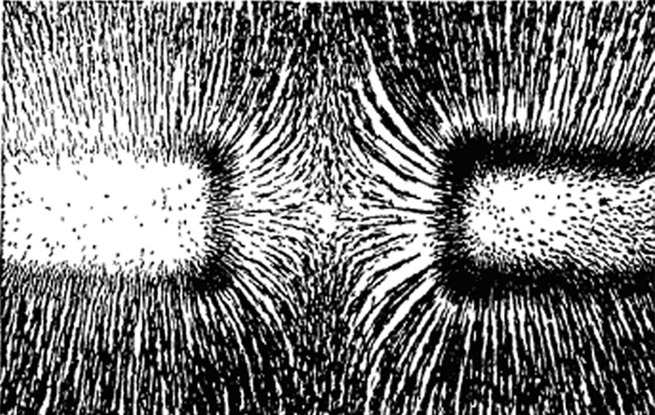
Diagram 14 magnetic repulsion lines between two like poles of a magnet as revealed with iron filings
While the attraction lines are a cross section of a torus these repulsion lines of force represent a cross section of another 3-d form which is the antithesis of the torus. These contrasting forms generated by the field lines manifest as attraction and repulsion. We can also hypothesize that the underling structure of these repulsion lines are bi-radial.
From the findings thus far it appears gravitation, and electromagnetism have the same underlying bi-radial structure. See part 5.
From the findings thus far it appears gravitation, and electromagnetism have the same underlying bi-radial structure. See part 5.
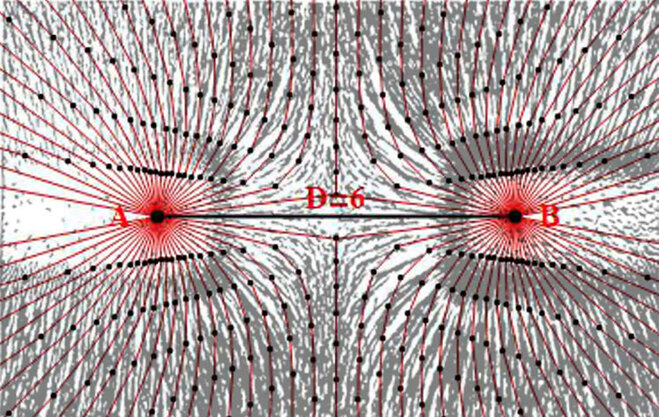Diagram 15
Here diagram 15 shows the bi-radial repulsion lines from diagram 13 highlighted in red and superimposed with traces of magnetic repulsion lines revealing the structural similarities between the two. Are there mathematical similarities also?
The underlying Structure of the Torus-yin and the counter Torus-Yang
The Hyperbolas
Diagram 16
The hyperbolas in the upper hemisphere of the bi-radial matrix each pass through the coordinates which have a constant ratio.
Part 4 Equations for the "lines of force"
Section 1 The attraction lines
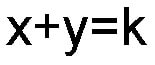Equation 1
From diagram 8 we can observe that the SUM of any bi-radial coordinates along a given attraction line is equal to a constant integer K. See the fifth layer for example where the set of bi-radial coordinates are: (5,1) (4,2) (3,3) (2,4) and (1,5). The sums of all these pairs being equal to 6. Also notice that in a bi-radial matrix where A=B. the equation x=y describes the set of nodes which runs perpendicular to and passes half way through the "D" segment.
Section 2 The repulsion lines
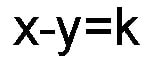Equation 2
From diagram 13 we can observe that the DIFFERENCE of any bi-radial coordinates on a given repulsion line is equal to a constant. Taking the 4th layer from pole "A" as an example we see that the coordinates along this repulsion line are: (5,1) (6,2) (7,3) and (8,4). The difference between these coordinates all being equal to 4. Just as attraction and repulsion are opposite so to the equation for attraction is based on addition, and the equation for the repulsion lines is based on subtraction.
Section 3 The Hyperbolas
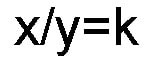Equation 3
From diagram 16 we can observe that in the upper hemisphere the RATIO or QUOTIENT of the coordinates along any given hyperbola is a constant. Notice that from equations 1,2 and 3 we can see that the fundamental field structures revealed in the bi-radial matrix are associated with the fundamental operators of addition, subtraction and division. This includes the well known attraction and repulsion fields. The hyperbola field to my knowledge has not been observed or investigated and is predicted by the bi-radial matrix.
PART 5
Geometrically Deriving a general bi-radial Inverse Square Equations
Section 1 Special case bi-radial matrix
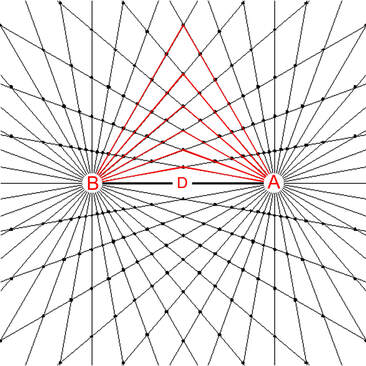Diagram 17A
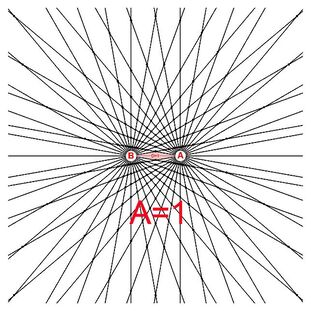
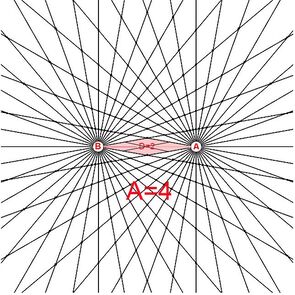
Note: diagram 1A shows a general inverse square law which applies to a wide range of phenomenon from gravity, radiation, electric fields, sound and virtually any single point source which spreads its influence equally in all directions. Diagram 17A extends this analogy to cover two point sources and highlights the interior radial segments where the number of rays from each pole A=36 and B=36.This model is a closer analogy to represent two significant gravitational masses. Like diagram 1A can the bi-radial symmetry describe a general inverse square relation over distance D? From there can this model be applied to various physical scenarios?
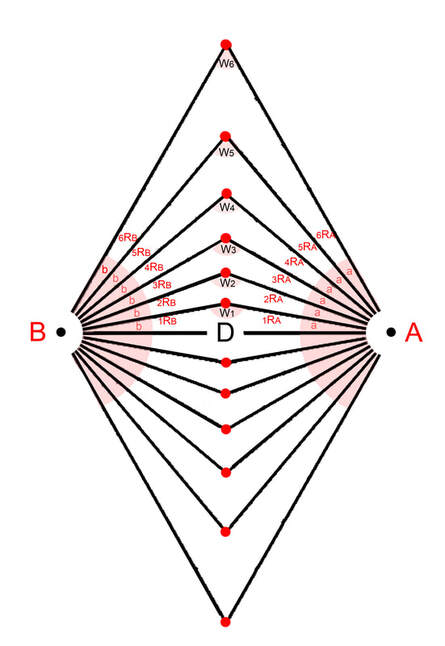Diagram 17B
Diagram 17B labels the interior angles and radial segments with variables for reference in the derivation of the following equations.
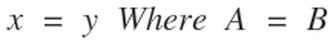Equation 3
Equation 3 equation for the vertical axis bisecting the D segment in diagram 17B where A = B. If A and B represent two equal masses the gravitational neutral zone would intersect the D segment half way between the two masses and the gravitational equilibrium line would run perpendicular to the D segment passing through this location.
Section 2 General case of the bi-radial matrix where A<B
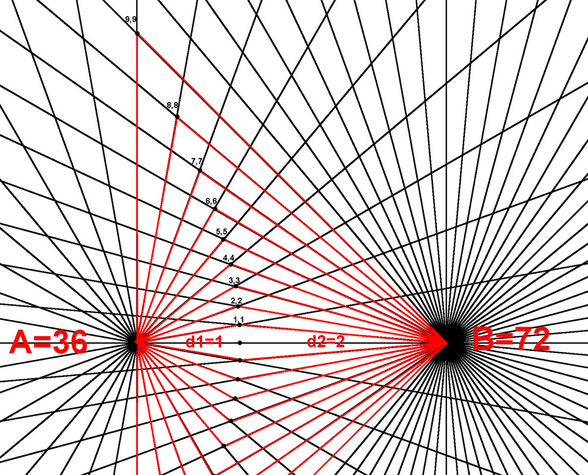Diagram 18A
To broaden its applications BRM needs to describe interactions between two unequal sources. In the general case BRM the number of rays from each pole differs being analogous to two different sized masses for instance. See diagram 18A. The interior radial segments are highlighted in red. These and the resulting interior angles are labeled in diagram 18B.
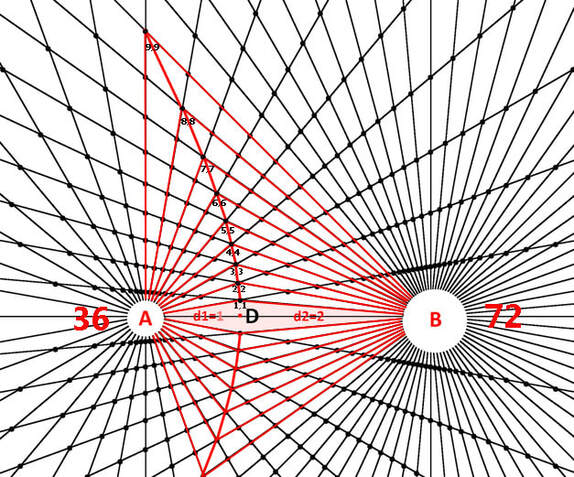Diagram 18B
Diagram 18B shows the interior radial segments of the general case bi-radial matrix where the number of rays from each pole differs corresponding to two unequal masses, A=36 and B=72 rays. Compare this to the special case in diagram 17 above. An inverse square equation applying to both the special case diagram 17B and the general case in diagram 18B is derived from the variables summarized below.
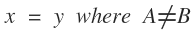Equation 4
From diagram 18B the equation x=y for the general case bi-radial matrix yields a different path because the initial values of "A" and "B" are not equal. Hence the line defined by x=y is a curve which is biased toward the smaller mass and intersects the D segment at a location where the segments on either side are approximately in the same proportion as the two masses. In this case 2:1. See diagrams 20, 21 and 22. This is qualitatively similar to the gravitational equilibrium zone between two unequal masses. This phenomenon relates to the gravitational equilibrium zone. Further variations of this matrix may pertain to the Lagrangian points. This is a very complex gravitational phenomenon and further parameters in the bi-radial matrix are required before being applied in this area of research.
Section 3 Summary of the variables
It turns out there are a number of inverse square relations over distance "D" in the bi-radial matrix. To derive a bi-radial based inverse square equations based on distance "D" between "A and "B" the variables established thus far are summarized. See diagrams 17B and 18B. Having determined structural similarities between the bi-radial matrix and electromagnetic lines of force and gravitational neutral zone can mathematical similarities be revealed as well? Could a fundamental equation of which known force equations are a special case be derived directly from this underlying structure? What is the correct analogy within the bi-radial matrix that corresponds to the "force" term in the fundamental inverse square laws?
Visual Geometric Description of Inverse square law
Diagram 18c
Diagram 18D
Diagram 18E
In Diagrams 18c-18E The inverse square relation is revealed in the area of the central diamond region. As the distance between the poles A and B increases linearly the area of the diamond region "A" increases per the square of the distance. The strength of the field in this region is inversely proportional to the area of the diamond. This is a direct geometric expression of Newtons inverse square law. This same diamond region can be described using trigonometry. The variables which have been introduced are indicated below.
Now Newton's inverse square law of gravity relates to the gravitational attraction between two masses. In the BRM this roughly corresponds to the pink shaded diamond region in diagrams 18A ,18B 18C, 18D, and 18E. In diagrams 18A and 18B as the number of rays increase about each pole A and B while maintaining the same proportion, in this case 2:1 the diamond shape flattens out and approaches a line segment. aka the D segment The first bi-radial inverse square equation uses the law of cosines to describe this region.
A revised list of variables now includes:
A= number of equi-spaced rays from pole "A"
B= number of equi-spaced rays from pole "B"
a= included angle around pole "A"
b=included angle around pole "B"
D= distance between "A" and "B"
WN=central angle(s)
NRA=length of Nth radial segment from pole "A"
NRB=length of Nth radial segment from pole "B"
A= number of equi-spaced rays from pole "A"
B= number of equi-spaced rays from pole "B"
a= included angle around pole "A"
b=included angle around pole "B"
D= distance between "A" and "B"
WN=central angle(s)
NRA=length of Nth radial segment from pole "A"
NRB=length of Nth radial segment from pole "B"
Preliminary equations
Equation 5
Equation 6
Equation 7
Equation 8
Equation 9
Equation 10
From Diagrams 17B, 18B and the law of cosines we have:
With substitutions from equations 9 and 10 we have:
Equation 11
bi-radial inverse square equation #1
PART 7
Relating the bi-radial inverse square equation #1 with inverse square force laws
Section 1 Comparing The Equations
Section 2 Preliminary Analysis
Equation 11 is a bi-radial general inverse square based equation over distance which is comparable to the three known inverse square force equations and is derived from the underlying structure. Is this precisely analogous to the three force equations? There is a "1" on the left side , that is a constant where the three force terms are variables. On the other side there is a variable term where in the force equations there is a constant Equation 11 is derived from a portion of the matrix (the inner diamond shape) and therefore is not a complete mathematical description of the entire field structure. If this equation were to be analogous to the three force equations it would suggest that the three force equations are only a partial expressions of their related fields to which they apply. There are a number of other inverse square relationships over distance in the bi-radial matrix. The basic thesis being proposed here is that the resemblance of the bi-radial field structures to actual field structures and the resemblance of the bi-radial inverse square equation to the known inverse square force equations is not a coincidence and that the structure of the force fields in the vicinity of these forces is bi-radial.
More extensive equations are needed to describe the entire toroidal and counter toriodal field structures. This model suggests that force is a quantum interference pattern.The force equations each have a constant: G, A and K whereas in equation 11 there is a variable expression. This is curious in light of variable gravitational constant. This also suggests a generalized equation which relates to all three forces. Also equation 11 contains both the sine and cosine functions which are wave functions. Does this indicate a wave function associated with gravity? A wave can be generally defined as the synthesis of rotational and linear displacement. Indeed the rotational displacement of time coupled with the linear displacement of space naturally forms a wave. This explains the underlying wave properties of the universe. In contrast the nodes concurrently exhibit the quantized particle properties of matter and force. What results does equation 11 yield when the length of the D segment approach zero or infinity coupled with variations in the ray count from both poles A and B?
Also the "1" on the left side of equation 11 requires physical interpretation. The force terms in the three force equations represent various units of measure. If we regard (1) as "unity" and as being analogous to a generalized force term we can say that force is the uniting of two quantum potentials into (1) field. We speak of force fields. This is because force IS a field with specific geometric form i.e. "lines of force" most prominently that of a torus and counter torus. The (1) thus represents (1) force field, primarily attraction or repulsion.* The BRM has revealed a detailed geometric analogy to force. See part 9, section 3.
More extensive equations are needed to describe the entire toroidal and counter toriodal field structures. This model suggests that force is a quantum interference pattern.The force equations each have a constant: G, A and K whereas in equation 11 there is a variable expression. This is curious in light of variable gravitational constant. This also suggests a generalized equation which relates to all three forces. Also equation 11 contains both the sine and cosine functions which are wave functions. Does this indicate a wave function associated with gravity? A wave can be generally defined as the synthesis of rotational and linear displacement. Indeed the rotational displacement of time coupled with the linear displacement of space naturally forms a wave. This explains the underlying wave properties of the universe. In contrast the nodes concurrently exhibit the quantized particle properties of matter and force. What results does equation 11 yield when the length of the D segment approach zero or infinity coupled with variations in the ray count from both poles A and B?
Also the "1" on the left side of equation 11 requires physical interpretation. The force terms in the three force equations represent various units of measure. If we regard (1) as "unity" and as being analogous to a generalized force term we can say that force is the uniting of two quantum potentials into (1) field. We speak of force fields. This is because force IS a field with specific geometric form i.e. "lines of force" most prominently that of a torus and counter torus. The (1) thus represents (1) force field, primarily attraction or repulsion.* The BRM has revealed a detailed geometric analogy to force. See part 9, section 3.
Section 3 Forming testable hypotheses from the bi-radial matrix
The BRM to be a viable model needs to be consistent with known physical properties and to make predictions which can be tested experimentally. It is known that between two masses there is a gravitational equilibrium zone where the gravitation from each mass cancel each other. Diagrams 2, 6, 8, 17B and 18B show geometrical formations which are consistent with this observation. Equation 3 shown below shows the bi-radial equation for this region and it falls along the line where the value of the bi-radial coordinates are equal. See part 6, section 3 for a review of the bi-radial gravitational equilibrium zone testable hypothesis.
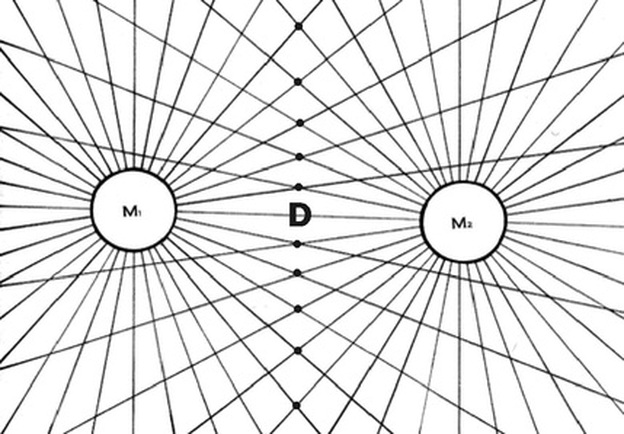Diagram 19
When the two masses are equal it would be expected that the gravitational equilibriuml zone would be equidistant from the centers of the two masses and perpendicular to the (D) axis between their two centers. There is a set of nodes in the BRM which corresponds to this.
The gravitational equilibrium zone and the bi-radial coordinate system
Diagram 20
The corresponding path for the gravitational equilibrium zone for two equal mass is along the line where the bi-radial coordinates satisfy the equation x=y in the matrix where A=B. In diagrams 19 and 20 A=36 and B=36.
The gravitational equilibrium zone between two unequal masses
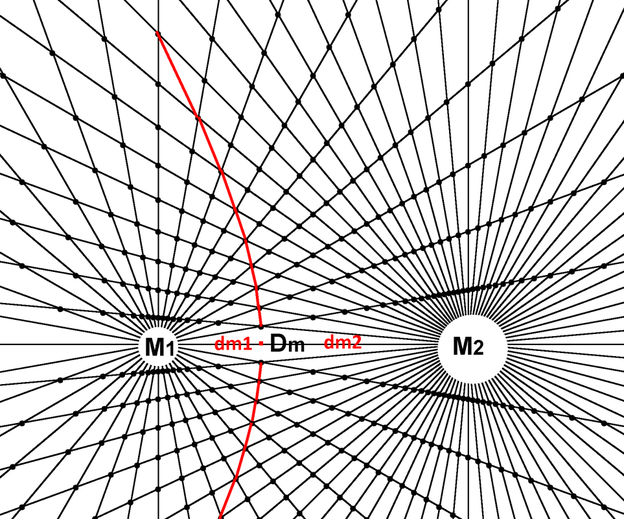Diagram 21
The gravitational equilibrium zone between two masses in an isolated two body system where A<B would be biased towards A and intersect the Dm segment closer to M1.
Co-ordinates of asymmetrical gravitational equilibrium zone where A<B
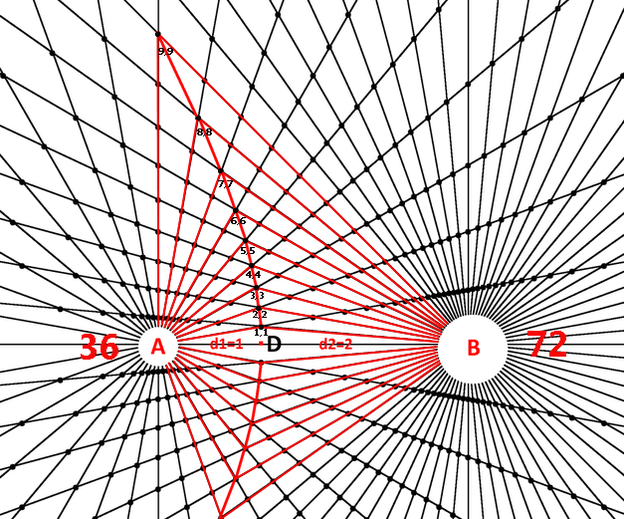Diagram 22
Diagram 22 represents the general case of the bi-radial matrix where "A" < "B". Here it would be expected that the gravitational equilibrium zone along the D segment would be closer to A than to B. It would be expected that the portion of the gravitational neutral zone off the D segment would be biased toward the smaller mass A owing to the "greater influence" of the larger mass. Here the interior radial segments from A and B are highlighted and the coordinates of the neutral zone are indicated. Notice the path defined by the equation x=y is biased towards pole A. The calculation of the gravitational neutral zone between two unequal masses is complicated and thus far we can state that the BRM predicts a gravitational neutral zone path which is qualitatively consistent with known data. In order to make more precise predictions of the Lagrangian points requires further research and development of the bi-radial matrix relating to the harmonic structure.This relates to the Lagrange points which involve difficult mathematical calculations and variables which are not currently included in the BRM. In further publications once the harmonic and near harmonic equations are worked out we speculate that the L1 point may fall along one of the higher quasi-harmonics.
1) The gravitational neutral zone between two isolated masses "Am and "Bm" with a distance between their centers Dm corresponds to the path defined by the bi-radial equation x=y in a bi-radial matrix where the number of radial lines from each pole in the matrix "A" and "B" are proportionate to the two masses A1 and B1 where D is the distance between the two poles is equal to Dm. Note the bi-radial equation a=b can be converted to Cartesian and other coordinate systems. Examples of this are shown in "Equations and Proofs drop down menu. A scaled down version of the BRM can be used to make the prediction. This achieves correct results when A=B.
Summarizing the gravitational equilibrium zone equations
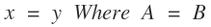
The equation for the vertical axis bisecting the D segment in diagram 19 where A = B.
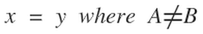
Here in diagram 21 the equation x=y for the general case BRM yields a different path because the initial values of "A" and "B" are not equal. Hence the line defining the gravitational neutral zone is a curve which is biased toward the smaller mass and intersects the D segment at a location where the segments on either side are in the same proportion as the two masses. In this case 2:1. See diagrams 21-24.
Additional hypothesis
2) That the underlying structure of electricity, magnetism and gravity is bi-radial. Deriving comparable field structures to the attraction and repulsion lines of force and a generalized inverse square equation directly from the bi-radial matrix from first principles supports this hypotheses.
Section 4 Bi-radial equivalence principle
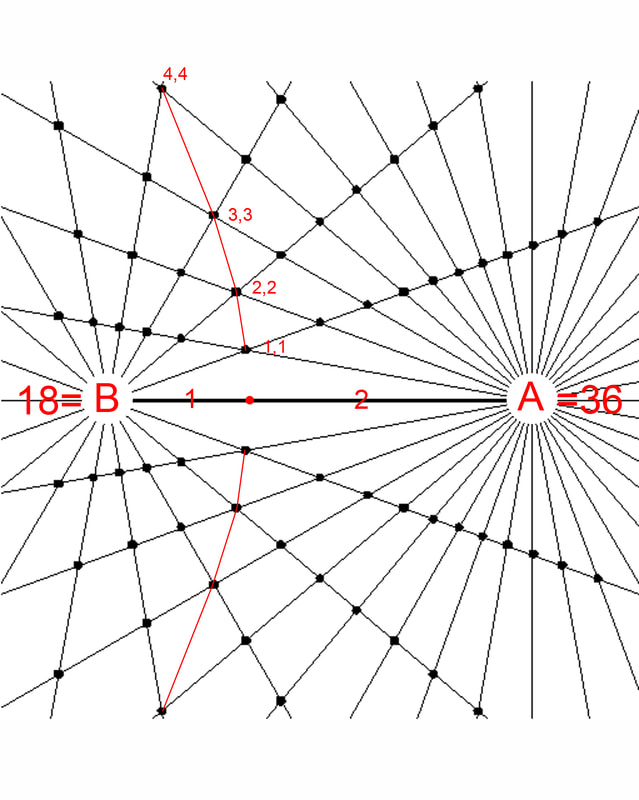Diagram 23
Here the BRM has 18 rays from pole A and 36 rays in pole B. As long as the ray numbers from each pole remain in the same proportion any given equation in the bi-radial matrix will define a set of nodes which fall along the same path. The distinction is in the sampling rate. This is an important feature of the bi-radial matrix.
In a bi-radial matrix the equation x=(f) y will define a set of nodes which falls on the same path as long as the ratio between the ray numbers from each pole remain the same.
Section 6 Unification of gravitation with electromagnetism
The BRM describes the underlying structure of two interacting gravitational fields as bi-polar; and obeying an inverse square law over distance. That the fundamental structure of gravitational interactions between two finite masses is bi-polar places gravity on the same geometric footing as electromagnetism. This could point the way to unification of gravitation with electromagnetism.
Diagram 24A
|
Electrical fields are at least bi-polar with the positive and negative poles being assigned the variables Q1 and Q2 or + and -. |
Diagram 24B
|
Magnetic fields are bi-polar and the poles are designated by P1 and P2 or N and S
|
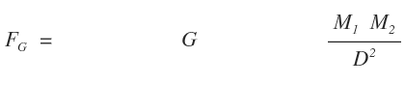
The structure of two interacting gravitational fields is bi-polar where the two poles are the centers of the two masses M1 and M2. With only one pole and corresponding mass Newton's equation breaks down. There is no distance (D) in the denominator and only one mass in the numerator.The BRM is clearly is an appropriate geometric analogy for Newton's inverse square law of gravitation for two masses.
PART 8 Deriving a universal scaling mechanism
Diagram 24C
Section 1 Back ground
Many researchers seek a common system or structure which is consistent with known physical properties from the microscopic to the macroscopic scale. Conformal field theories have similar properties of invariance. Earlier pioneers including Einstein and Weyl proposed classical unified field theories which attempted to find a common expression for quantum physics and general relativity (microscopic vs macroscopic) and to unify gravitation with electromagnetism. It is known that the atomic and sub-atomic forces are much stronger and exert over minute distances. It is known that gravity is much weaker and exerts over vast distances. Finding a single internally consistent geometric structure which serves as a complete analogy and description of both these conditions has been elusive. Recently a greater interest in detailed geometrical scaling models has emerged in the technical literature.
Many researchers seek a common system or structure which is consistent with known physical properties from the microscopic to the macroscopic scale. Conformal field theories have similar properties of invariance. Earlier pioneers including Einstein and Weyl proposed classical unified field theories which attempted to find a common expression for quantum physics and general relativity (microscopic vs macroscopic) and to unify gravitation with electromagnetism. It is known that the atomic and sub-atomic forces are much stronger and exert over minute distances. It is known that gravity is much weaker and exerts over vast distances. Finding a single internally consistent geometric structure which serves as a complete analogy and description of both these conditions has been elusive. Recently a greater interest in detailed geometrical scaling models has emerged in the technical literature.
Section 2 Bi-radial matrix model on microscopic scale
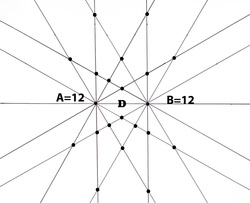Diagram 25
Diagram 25 is a bi-radial matrix with two poles showing 12 rays from poles "A" and "B" corresponding to smaller masses. A general property of the bi-radial matrix which has been proven mathematically is that for a given distance "D" between "A" and "B" a smaller amount of rays from each pole decreases the "range" of the matrix This means for instance that in diagram 25 the set of nodes in the matrix is limited to a short range. Also given a fixed number of rays from each pole as the distance D between the poles decreases the range of the matrix decreases. The attraction lines are shown in diagram 26 showing a field with limited range.
Interference pattern of bi-radial matrix with low ray numbers
Diagram 26
Diagram 25 depicts a bi-radial interference pattern where the number of rays is small and the distance between A and B is extremely short.
Bi-radial scaling function on microscopic scale
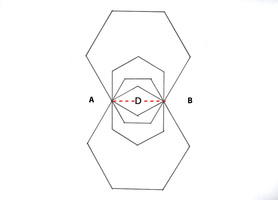
Diagram 27
Connecting the nodes in diagram 26 forms the attraction lines. While the smaller ray numbers from each pole tends to increase the spacing between the nodes and the resulting attraction lines and lower the density of the field, as the distance decreases to the atomic and sub-atomic scale the distance factor supersedes the ray number factor and the resulting field is highly concentrated yet only exists over a small region. This is the same property of atomic and sub-atomic forces.
Section 3 Bi-Radial scaling function on a macroscopic scale
Diagram 28
While a larger ray number count from both poles corresponding to larger masses tends to increase the population density of the fields lines and nodes within the matrix corresponding to a stronger field, when the distance between the two poles becomes astronomical in scale (note shown) the distance factor supersedes the ray number factor and lowers the density of the field in the interaction region while the field extends over a vast distance. This is completely analogous with and corresponds to gravity.
Notice with the higher ray count from poles A and B there is a finer interference pattern which is not decipherable with lower ray numbers.
Notice with the higher ray count from poles A and B there is a finer interference pattern which is not decipherable with lower ray numbers.
PART 9 Reciprocal Harmonic structure of space time
Section 1 Isolating the reciprocal harmonic structure
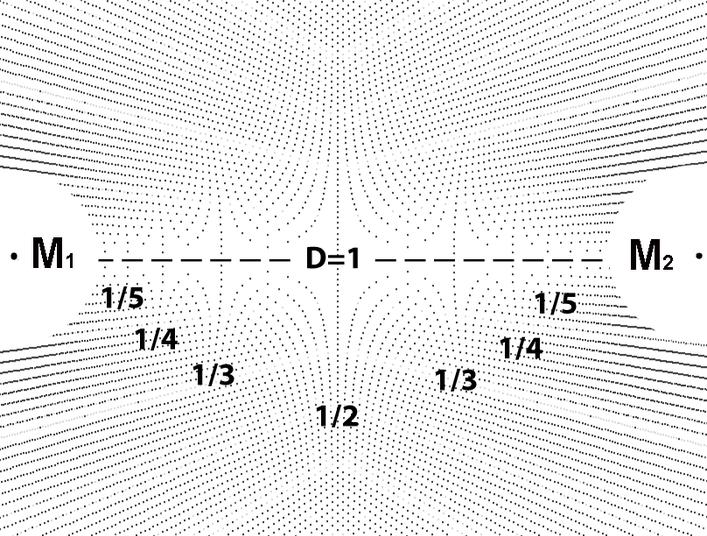Diagram 29
Isolating the nodes in diagram 28 we see there are seemingly hyperbolic lines which intersect the D segment between the two poles along with a vertical axis bisecting the D segment. The equations of these lines are easily derived from the matrix. See below. The intervals at which the hyperbolic and asymptotic curves approach the D segment correspond to the harmonic series within visual tolerances as shown in diagram 29.
The underlying near harmonic structure of the bi-radial matrix is consistent with known properties of atoms: "The realization that atoms are vibrating in motions that are nearly harmonic is essential for understanding many properties of matter including molecular spectra, heat capacity and heat conduction." The near harmonic vibration of atoms can be attributed to their near harmonic structure. Is there a mathematical equation from the Bi-Radial matrix which can confirm this? To do so we need to view a bi-radial matrix with a lower ray sampling rate. Also note in the "Equations and Proofs" section there is the Cartesian based equation describing one of these curves.
The underlying near harmonic structure of the bi-radial matrix is consistent with known properties of atoms: "The realization that atoms are vibrating in motions that are nearly harmonic is essential for understanding many properties of matter including molecular spectra, heat capacity and heat conduction." The near harmonic vibration of atoms can be attributed to their near harmonic structure. Is there a mathematical equation from the Bi-Radial matrix which can confirm this? To do so we need to view a bi-radial matrix with a lower ray sampling rate. Also note in the "Equations and Proofs" section there is the Cartesian based equation describing one of these curves.
Reciprocal relation between time and space as expressed with numbers
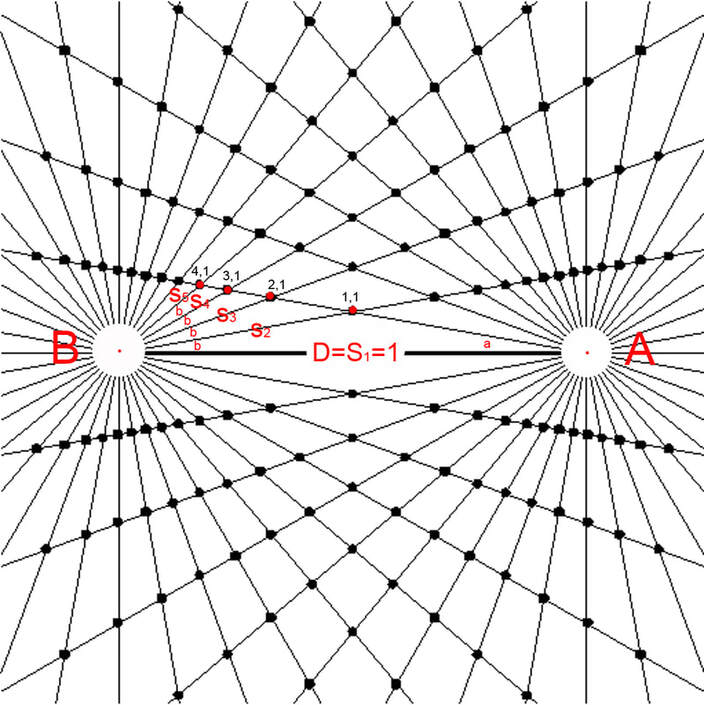Diagram 30
Notice in diagram 30 the set of "S" segments. This is a different set than the previous set of "R" segments used in the Bi-radial inverse square equation. Here the "S" segments have their origin at "B". There is a similar mirror set of "S" segments whose origin is at "A".
Section 2 Bi-Radial harmonic equation
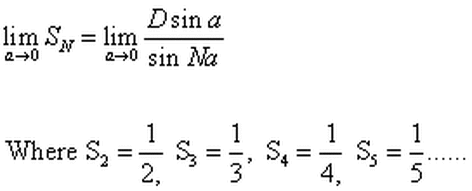
EQ 12
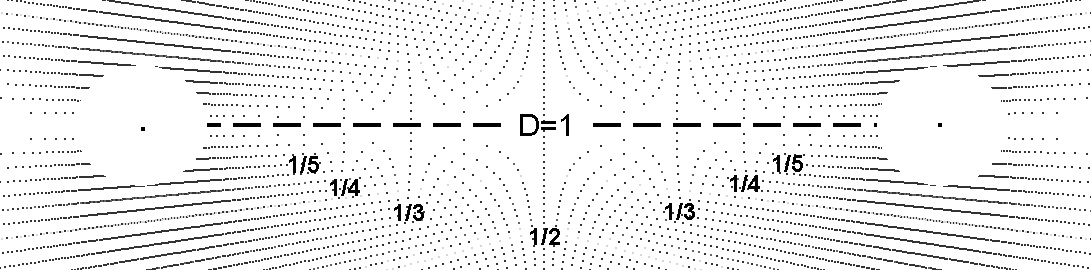
From diagram 30 equation 12 indicates the near harmonic structure of the BRM. It suggests that as the number of equi-spaced rays from each pole "A" and "B" (when A=B) approach infinity the exact harmonic series is attained. Here the units of time are counting numbers: 1,2,3... representing the discrete unitized angular (pie) sections and the
spatial linear sections are the ratios of the harmonic series: 1, 1/2, 1/3, 1/4... When A≠B as A and B approach infinity a whole range of variations to the harmonic series result requiring separate analyses.
spatial linear sections are the ratios of the harmonic series: 1, 1/2, 1/3, 1/4... When A≠B as A and B approach infinity a whole range of variations to the harmonic series result requiring separate analyses.
Section 3 Analyzing the harmonic field structure of the bi-radial matrix.
The hyperbolas pass through unique sets of nodes. The coordinates within each pairing relate to the harmonic overtone series or their reciprocals. For any given coordinate located on a hyperbola (x,y) the ratio x/(x+y) yields either a harmonic ratio or its reciprocal and indicates the portion of the D segment that hyperbola approaches. For example applying the formula x/(x+y) to the coordinate (8,4) yields the ratio 8/(8+4) or 2/3. If we start at pole "B" the hyperbola which passes through (8,4) approaches the D segment at 2/3 of its length.
Diagram 31
Section 4 Equation for hyperbolas
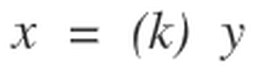Equation 13
As previously indicated It turns out that that the quotient of the coordinates along the hyperbolas yields a constant. To verify these curves are (asymptotic) hyperbolas a Cartesian equivalent is described in the equations and proofs section. The hyperbolas pass through unique sets of nodes. The ratios of the of the coordinates within each pairing relate to the harmonic overtone series or their reciprocals. This is completely analogous to the D segment being a vibrating string of unit length and the various sub-divisions and coordinate pairings representing the harmonic overtones. See Part 9 section 5 reviewing harmonic coordinate conditions. See part 9 section 3 for comparison to string theory.
Bi-radial matrix as distance between poles approaches zero with high ray counts corresponding to large masses
Diagram 32 Bi-radial matrix with high ray number and distance "D" approaching zero
Diagram 32 shows a BRM with high number of rays relative to the distance between the poles "A" and "B" which approaches zero (singularity). Notice the attraction lines in relationship to the two sets of equi-spaced radial lines.The harmonic structure which is detailed in diagram 30 is less obvious and still present even as the distance between the poles approaches zero. See part 9 section 8.
PART 9 The bi-radial matrix, existing theories, models and concepts
This section focuses on the common features of existing theories and models with the BRM
Section 1 Quantum Geometry
In the quest to develop quantum geometry, from 1947, researchers were attempting to quantize space-time so that the resulting coordinates would not be ordinary real numbers, but rather elevated to "quantum operators" obeying some nontrivial quantum non-commutativel relations. Hence the term "non-commutative geometry". The BRM is a viable example of a commutative quantum geometry which is able to use real numbers as coordinates and revealing electromagnetic and gravitational field structures and anomalous physical phenomenon on the microscopic and macroscopic scale. Elaborating on his previous quote Penrose continues:
"...My idea is to try to reformulate" physical laws so that they may be expressed entirely in terms of quantities which are discrete according to quantum physics. These reformulated" laws would, hopefully, be expressible entirely in combinatorial terms, even though they would be essentially re-expressing the content of conventional quantum theory, of space-time theory and, perhaps, of other aspects of physics as well. Thus, the quantum theory and space-time theory would be expected to arise together, out of some more primitive combinatorial theory..."
The BRM has basic components of lines and angles representing space and time which combine in various ways to form fundamental field structures from which fundamental equations directly emerge. This certainly has the properties of a more "primitive combinatorial theory" giving rise to fundamental symmetries, harmonic and inverse square relationships consistent with known physical laws.
"...My idea is to try to reformulate" physical laws so that they may be expressed entirely in terms of quantities which are discrete according to quantum physics. These reformulated" laws would, hopefully, be expressible entirely in combinatorial terms, even though they would be essentially re-expressing the content of conventional quantum theory, of space-time theory and, perhaps, of other aspects of physics as well. Thus, the quantum theory and space-time theory would be expected to arise together, out of some more primitive combinatorial theory..."
The BRM has basic components of lines and angles representing space and time which combine in various ways to form fundamental field structures from which fundamental equations directly emerge. This certainly has the properties of a more "primitive combinatorial theory" giving rise to fundamental symmetries, harmonic and inverse square relationships consistent with known physical laws.
Section 2 A New Kind of Science
Within the vast scope of Stephen Wolfram's work he addresses challenging problems in quantum physics, gravitation and matter emphasizing an underlying structure or network. The following quote regarding matter and gravity from Wolfram in "A New Kind of Science" is indicative of his approach and resonates with the findings in this presentation:
"...But why exactly does matter have to be introduced explicitly at all? It has been the assumption of traditional physics that even though gravity can be represented in terms of properties of space, other elements of our universe cannot. But in my approach everything just emerges from the same underlying network- or in effect from the structure of space..."
Concerning Quantum theory he further elaborates:
" The full mathematical structure of quantum field theory is far from completely worked out. But the basic notion is that for each possible type of particle there is some kind of continuous field that exists through out space-with the presence of a particle corresponding to a simple type of structure in this field."
Concerning space, time and the laws of physics he states:
"...But now instead of defining constraints just in space, the laws of physics can be thought of as defining constraints on what can happen in both space and time....Just as for space it is my strong belief that time is fundamentally discrete..."
The bi-radial matrix represents an underlying structure which is consistent with these descriptions and more correlations are emerging from the present investigation. A further generalization of the BRM involving N-poles gives a more detailed description of atomic structure "...defining constraints on what can happen in both space and time."
"...But why exactly does matter have to be introduced explicitly at all? It has been the assumption of traditional physics that even though gravity can be represented in terms of properties of space, other elements of our universe cannot. But in my approach everything just emerges from the same underlying network- or in effect from the structure of space..."
Concerning Quantum theory he further elaborates:
" The full mathematical structure of quantum field theory is far from completely worked out. But the basic notion is that for each possible type of particle there is some kind of continuous field that exists through out space-with the presence of a particle corresponding to a simple type of structure in this field."
Concerning space, time and the laws of physics he states:
"...But now instead of defining constraints just in space, the laws of physics can be thought of as defining constraints on what can happen in both space and time....Just as for space it is my strong belief that time is fundamentally discrete..."
The bi-radial matrix represents an underlying structure which is consistent with these descriptions and more correlations are emerging from the present investigation. A further generalization of the BRM involving N-poles gives a more detailed description of atomic structure "...defining constraints on what can happen in both space and time."
Section 3 General inverse square law
The BRM is a logical out growth of the general inverse square law relating to surface area of a sphere compared to its radius.. It is similar in that it is of purely geometric origin and shows close parallels to physical phenomenon. Where as the general inverse square law applies to single point source phenomenon such as a point source of light or a single gravitational mass, the BRM applies to bi-polar systems and two body systems. Further extensions of the BRM with multiple poles can apply to the many body and n-body problems. Just as mathematical inverse square relationship over distance is derived from the expanding sphere model relating its surface area to its radius with numerous parallels in physics, another mathematical inverse square relationship over distance is derived directly from the BRM symmetry with wide applications in physics most notably in the analysis of complex field structures.
Section 4 String Theory
While string theory is highly complex and controversial it has some basic concepts which are consistent with the bi-radial matrix relating to the importance of harmonics and vibration relating to the basic forces in nature. While the bi-radial matrix is based on an entirely different premise and set of assumptions than string theory the phenomenon of harmonics along with the analogy of a vibrating string is central to both systems. This following passage by noted String theorist Edward Witten describing part of string theory is especially interesting in light of diagram 30: "In string theory, different harmonics correspond to different particles. If string theory proves correct, all elementary particles-electrons, photons, neutrinos, quarks and the rest-owe their existence to subtle differences in the vibration of strings.The theory offers a way to unite disparate particles because they are in essence, different manifestations of the same basic string." If we regard the distance "D" between the two poles as unity (D=1) as shown through out this presentation than the sub-divisions of the rays as the number of rays from each pole approach infinity, each approach the ratios of the harmonic overtones or combinations therein. This would make the D segment analogous to a vibrating string of unit length. The nodes which fall along the hyperbolas in diagram 30 have coordinates which correspond to the harmonic overtone ratios of a vibrating string. In string theory the length of the string is sub-microscopic where as in the bi-radial matrix the length of the D segment (analogous to the vibrating string) covers the full range between microscopic and macroscopic.
Section 5 Harmonics
Harmonics is a vast field of study covering a wide range of phenomenon from music to physics to plant morphology. Here we are concerned with a particular aspect relating to the properties of a vibrating string.
Diagram 32A
|
Diagram 32B
|
|
An un-teathered string
An un-tethered string is incapable of harmonic vibration. |
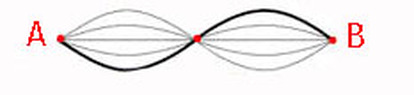
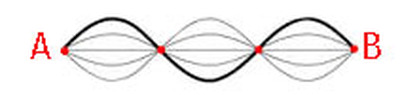
Second harmonic or first overtone - f2
It is only when the string is anchored down on both ends and brought to sufficient tension is it capable of sonorous harmonic vibration. The anchor points are "A" and "B" and they together are potentials. These correspond to the Poles "A" and "B" in the bi-radial matrix. |
 Diagram 32C
Second harmonic or first overtone - f2 |
 Diagram 32D
Third harmonic or second overtone - f3 |
Diagram 33
This basic algorithm which illustrates divisibility and a reflective symmetrical structure of the counting numbers also illustrates how counting numbers parallel the reciprocal harmonic relation between space and time.
When sampling the two (2) column sequentially starting at one (1) a white square occurs every two spaces 2(S) and thus occurs one half of the time 1/2(T).
When sampling the three (3) column sequentially starting at one (1) a white square occurs every three spaces (3S) and thus occurs one third of the time 1/3(T).
When sampling the four (4) column sequentially starting from one (1) a white square occurs every four spaces (4S) and thus occurs one fourth of the time 1/4(T).
Like the BRM this shows the reciprocal harmonic relation between space and time with one major difference. In this case space is unitized and time is non-unitized (integer vs real).
When sampling the two (2) column sequentially starting at one (1) a white square occurs every two spaces 2(S) and thus occurs one half of the time 1/2(T).
When sampling the three (3) column sequentially starting at one (1) a white square occurs every three spaces (3S) and thus occurs one third of the time 1/3(T).
When sampling the four (4) column sequentially starting from one (1) a white square occurs every four spaces (4S) and thus occurs one fourth of the time 1/4(T).
Like the BRM this shows the reciprocal harmonic relation between space and time with one major difference. In this case space is unitized and time is non-unitized (integer vs real).
Section 6 Coordinate Systems
A number of coordinate systems are presently used in physics the most prevalent being the Cartesian coordinate system with variations to include a fourth time coordinate. Other coordinate systems with multiple origins including the bi-radial matrix are more revealing in cases where the underlying symmetry of the phenomenon corresponds to the symmetry of the coordinate system. This is the case with the bi-radial coordinate system with respect to two interacting gravitational fields and magnetism where the bi-polar symmetry of the respective forces correspond to the A and B origins of the BRM. This also greatly simplifies the attendant mathematics. The BRM gives rise to a harmonic coordinate system. This is worth considering in light of the harmonic coordinate condition which is among several coordinate conditions used in general relativity to solve the Einstein field equations.
The BRM is an alternative frame work and coordinate system among several alternatives to the Cartesian coordinate system to evaluate various experimental and observational scenarios. It appears more appropriate than the Cartesian coordinate system to evaluate the phenomenon of force fields which as a general rule are bi-polar or even multi-polar and quantized in nature. It appears better suited to formulate a quantum geometry to investigate these phenomenon owing to its discrete properties versus a continuous infinitely divisible space. David Bohm's views on the Cartesian coordinate system are summarized by F. David Peat :
"Bohm argued the Cartesian order was incompatible with the new insights into quantum theory. The Cartesian grid is abstract and arbitrary; has no deep ontological connection with the quantum world. Moreover, he said, it assumes the existence of infinitesimal points within a continuous, infinitely divisible space. This assumption is incompatible with the basic insights into quantum theory, in which the notion of space breaks down long before the domain of the dimensionless point is reached. A revolution has occurred in physics, but at a deeper level the same order has prevailed. The new wine of quantum theory has merely been put in the old bottles of the Cartesian order."
The Cartesian coordinate system lends itself to a background dependent view of physics which has long since been superseded by both relativity, and subsequent theories and models. As indicated previously there is a companion matrix which has inverse properties to the bi-radial matrix which can be adapted to yet another alternative coordinate system and is more suited than the bi-radial matrix for other experimental and observational scenarios including the Young double slit experiment.There are a myriad of other coordinate systems including the standard (mono) polar coordinate system. There are triangular coordinate systems and many others. In light of all the varied coordinate systems available we consider it vital to be open minded and thorough in the selection process as to which coordinate system to employ in any given experimental, observational or theoretical scenario. Also like the polar coordinate system the bi-radial matrix-coordinate system can be converted to Cartesian and other coordinate systems.
The BRM is an alternative frame work and coordinate system among several alternatives to the Cartesian coordinate system to evaluate various experimental and observational scenarios. It appears more appropriate than the Cartesian coordinate system to evaluate the phenomenon of force fields which as a general rule are bi-polar or even multi-polar and quantized in nature. It appears better suited to formulate a quantum geometry to investigate these phenomenon owing to its discrete properties versus a continuous infinitely divisible space. David Bohm's views on the Cartesian coordinate system are summarized by F. David Peat :
"Bohm argued the Cartesian order was incompatible with the new insights into quantum theory. The Cartesian grid is abstract and arbitrary; has no deep ontological connection with the quantum world. Moreover, he said, it assumes the existence of infinitesimal points within a continuous, infinitely divisible space. This assumption is incompatible with the basic insights into quantum theory, in which the notion of space breaks down long before the domain of the dimensionless point is reached. A revolution has occurred in physics, but at a deeper level the same order has prevailed. The new wine of quantum theory has merely been put in the old bottles of the Cartesian order."
The Cartesian coordinate system lends itself to a background dependent view of physics which has long since been superseded by both relativity, and subsequent theories and models. As indicated previously there is a companion matrix which has inverse properties to the bi-radial matrix which can be adapted to yet another alternative coordinate system and is more suited than the bi-radial matrix for other experimental and observational scenarios including the Young double slit experiment.There are a myriad of other coordinate systems including the standard (mono) polar coordinate system. There are triangular coordinate systems and many others. In light of all the varied coordinate systems available we consider it vital to be open minded and thorough in the selection process as to which coordinate system to employ in any given experimental, observational or theoretical scenario. Also like the polar coordinate system the bi-radial matrix-coordinate system can be converted to Cartesian and other coordinate systems.
Section 7 Loop Quantum Gravity
This theory advances the concept that space-time is quantized and the theory as a whole is background independent. From this a description of quantum gravity is pursued integrating quantum mechanics with general theory of relativity. One of the methods used to describe this are "spin networks. "It is quite astonishing to note the following description of Loop Quantum Gravity in light of the bi-radial matrix diagrams through out this presentation:
"In short, the spin network approach from loop quantum gravity shows spacetime as a series of pieces that are connected to each other. This can be visualized by dots (or nodes) representing the pieces of spacetime connected by lines - in other words, spacetime can be viewed as a network of quantum nodes. The smooth spacetime framework explicit in general relativity is what you see when you "zoom out" from the quantum scale up to the larger scale."
While the BRM looks different than the spin-network diagrams devised by Penrose the similarities are telling. The description given of the spin network generally describes the BRM! As the number of rays from each pole in the bi-radial matrix approaches infinity, representing larger masses the line segments connecting the nodes and forming the field lines become shorter and shorter to the extent that the curvature appears more and more continuous. As the number of rays from each pole in the bi-radial matrix decreases corresponding to smaller masses the discrete quantized structure becomes more evident.
The theory of loop quantum gravity, describes the fabric of space-time as an evolving spider's web of strands that carry information about the quantized areas and volumes of the regions they pass through. The individual strands of the web must eventually join their ends to form loops, hence the theory's name. Not to be confused with the much better known strings of string theory which move around in space-time. Strands actually are space-time: the information they carry defines the shape of the space-time fabric in their vicinity. Could the non-concentric circles in diagrams 12A and 12B correspond to these loops?
One of the founders of Loop Quantum Gravity Lee Smolin has proposed in his recent book "Time Re-born" that Time is fundamental and space is an emergent feature. This contrasts previous notions of time and space where time is an emergent property of space. This points to the compelling need to clarify the relation between space and time. The BRM represents a time based system which accurately mimics many experimental and observational scenarios including force field structures. As cited earlier there is companion matrix to the BRM which is analogous to time being an emergent property of space and our research indicates that his matrix applies to other experimental and observational scenarios including the Young double slit experiment.
"In short, the spin network approach from loop quantum gravity shows spacetime as a series of pieces that are connected to each other. This can be visualized by dots (or nodes) representing the pieces of spacetime connected by lines - in other words, spacetime can be viewed as a network of quantum nodes. The smooth spacetime framework explicit in general relativity is what you see when you "zoom out" from the quantum scale up to the larger scale."
While the BRM looks different than the spin-network diagrams devised by Penrose the similarities are telling. The description given of the spin network generally describes the BRM! As the number of rays from each pole in the bi-radial matrix approaches infinity, representing larger masses the line segments connecting the nodes and forming the field lines become shorter and shorter to the extent that the curvature appears more and more continuous. As the number of rays from each pole in the bi-radial matrix decreases corresponding to smaller masses the discrete quantized structure becomes more evident.
The theory of loop quantum gravity, describes the fabric of space-time as an evolving spider's web of strands that carry information about the quantized areas and volumes of the regions they pass through. The individual strands of the web must eventually join their ends to form loops, hence the theory's name. Not to be confused with the much better known strings of string theory which move around in space-time. Strands actually are space-time: the information they carry defines the shape of the space-time fabric in their vicinity. Could the non-concentric circles in diagrams 12A and 12B correspond to these loops?
One of the founders of Loop Quantum Gravity Lee Smolin has proposed in his recent book "Time Re-born" that Time is fundamental and space is an emergent feature. This contrasts previous notions of time and space where time is an emergent property of space. This points to the compelling need to clarify the relation between space and time. The BRM represents a time based system which accurately mimics many experimental and observational scenarios including force field structures. As cited earlier there is companion matrix to the BRM which is analogous to time being an emergent property of space and our research indicates that his matrix applies to other experimental and observational scenarios including the Young double slit experiment.
Section 8 Quantum potentials, non-locality, Implicate order
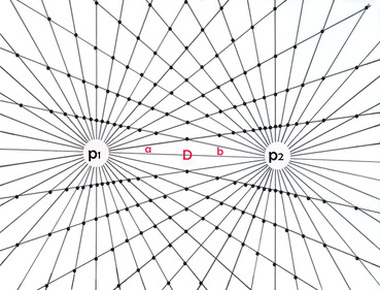Diagram 34
David Bohm et al have introduced the concept of the "quantum potential", "non-locality" and "The Implicate Order". Here we simply introduce a geometric representation of a quantum potential and define any set of equi-spaced radial lines as a quantum "time" potential.
Axiom: time without space exists only as a potential. When a second time potential is introduced it creates a space "D" between them. See diagram 34.
Time has been expressed as equi-spaced angular increments for thousands of years and is manifested in the face of clocks. These evolved from sun dials which were an indicator of the Earths rotation in relation to the suns rays. Time as we know IS rotation defined by discrete equi-spaced angular increments based on two reference systems.*
The bi-Radial matrix then is a useful model of "space-time". This indicates that gravitational and magnetic fields can be described in terms of interference patterns between two "quantum potentials". A more detailed treatment of this is beyond the scope of this introduction. Here the goal is to indicate the possible applications of the bi-radial matrix. Non-locality does have an expression in the BRM and this requires an additional variable (the phase relation) in order to be accurately described. This involved the rotation of This will be covered in future presentations.
Axiom: time without space exists only as a potential. When a second time potential is introduced it creates a space "D" between them. See diagram 34.
Time has been expressed as equi-spaced angular increments for thousands of years and is manifested in the face of clocks. These evolved from sun dials which were an indicator of the Earths rotation in relation to the suns rays. Time as we know IS rotation defined by discrete equi-spaced angular increments based on two reference systems.*
The bi-Radial matrix then is a useful model of "space-time". This indicates that gravitational and magnetic fields can be described in terms of interference patterns between two "quantum potentials". A more detailed treatment of this is beyond the scope of this introduction. Here the goal is to indicate the possible applications of the bi-radial matrix. Non-locality does have an expression in the BRM and this requires an additional variable (the phase relation) in order to be accurately described. This involved the rotation of This will be covered in future presentations.
Section 9 Black holes and Super Gravity
It is interesting to note that some have suggested that so called black holes are not pure singularities and that they have two centers approaching but never reaching zero distance or singularity. While there are alternative explanations to account for the regions known as black holes it is interesting to note in light of diagrams 27, 29 and 30 the harmonic relationships occurring in these regions as cited by various investigators:
"The non-linear generation of harmonics in gravitational perturbations of black holes is explored using numerical relativity based on an in-going light-cone framework."
Philippos Papadopoulos
"The Harmonic Structure of High-Frequency Quasi-periodic Oscillations in Accreting BlackHoles"
Title of article by Jeremy D. Schnittman and and Edmund Bertschinger
"Simulations of highly distorted black holes provide us with a suitable system to investigate the generation of nonlinear harmonics in black-hole oscillations."
From abstract by Shoemaker, Deirdre; Pfeiffer, Harald; Kidder, Larry; Teukolsky, Saul
The BRM indicates a field structure that approaches the harmonic series as the ray numbers approach infinity, corresponding to larger mass. It is workable model on macroscopic scale in extreme gravity scenarios.
"The non-linear generation of harmonics in gravitational perturbations of black holes is explored using numerical relativity based on an in-going light-cone framework."
Philippos Papadopoulos
"The Harmonic Structure of High-Frequency Quasi-periodic Oscillations in Accreting BlackHoles"
Title of article by Jeremy D. Schnittman and and Edmund Bertschinger
"Simulations of highly distorted black holes provide us with a suitable system to investigate the generation of nonlinear harmonics in black-hole oscillations."
From abstract by Shoemaker, Deirdre; Pfeiffer, Harald; Kidder, Larry; Teukolsky, Saul
The BRM indicates a field structure that approaches the harmonic series as the ray numbers approach infinity, corresponding to larger mass. It is workable model on macroscopic scale in extreme gravity scenarios.
Section 10 Classical Unified field theories
As noted above Einstein, Weyl and others sought to unify Gravitation with electromagnetism. This was in pursuit of classical unified field theories. It is important to note that the reason the strong and weak forces were postulated was due to the fact that the atomic and sub-atomic forces were not obeying the inverse square relations as depicted in the fundamental force equations shown above. It was initially thought that subatomic forces could be accounted for with electromagnetism. This will be addressed in further presentations.
Einstein described a gravitational field as curvature of the space time continuum around a mass. He also sought to incorporate quantum theory as part of his unification efforts. In general he was defining force in terms of space and time. The bi-radial matrix thus defines a space-time "dis-continuum" and arrives at a geometric description of force in terms of space and time. Part 3, section 3. In the bi-radial matrix there are only straight segments defining the spatial displacements and only straight rays defining the angular time displacements. The segments connecting the nodes forming the field lines are straight also. The apparent curvature represent the paths along which the segments connecting the nodes coincide. As the number of rays from each pole approach infinity the the segments forming the field lines become shorter and shorter, and their aggregate approaches but never attains a continuous curve.
Einstein described a gravitational field as curvature of the space time continuum around a mass. He also sought to incorporate quantum theory as part of his unification efforts. In general he was defining force in terms of space and time. The bi-radial matrix thus defines a space-time "dis-continuum" and arrives at a geometric description of force in terms of space and time. Part 3, section 3. In the bi-radial matrix there are only straight segments defining the spatial displacements and only straight rays defining the angular time displacements. The segments connecting the nodes forming the field lines are straight also. The apparent curvature represent the paths along which the segments connecting the nodes coincide. As the number of rays from each pole approach infinity the the segments forming the field lines become shorter and shorter, and their aggregate approaches but never attains a continuous curve.
Section 11 Conformal Field Theory
Conformal field theories are quantum field theories that are invariant under conformal transformations. These are transformations of the underlying space-time that leave angles unchanged, but not necessarily lengths. In particular these theories are invariant under a re-scaling of all distances. This is the exact property of the bi-radial matrix where all the internal angles of the trapezoids remain unchanged regardless of scale as determined by the length of the D segment. (Diagrams 2,3 and 5). The bi-radial structure is fundamental and directly represents the geometric relation between space and time. From this underlying harmonic structure the characteristic field structures and basic mathematical relations are derived from first principles.
Section 12 Interactive demonstration of the bi-radial matrix
For an interactive demonstration of the bi-radial matrix including animations click on the following link and see information on downloading the link: http://demonstrations.wolfram.com/BiradialMatrix/
Once on the Wolfram site follow the prompts to down load the CDF player.
For an interactive demonstration of the bi-radial matrix including animations click on the following link and see information on downloading the link: http://demonstrations.wolfram.com/BiradialMatrix/
Once on the Wolfram site follow the prompts to down load the CDF player.
Summary
Diagram 35 bi-radilal matrix interference pattern with with interior harmonic structure
See diagram A bi-radial matrix was constructed as a logical extension to an existing model of gravitation. A bi-radial coordinate system was logically derived to facilitate further analysis. An interference pattern was formed from isolating the intersection nodes. A series of connection algorithms were implemented and fundamental attraction, repulsion and hyperbolic force field structures derived from first principles. Basic equations defining the lines of force were derived.
“ On a small enough scale space is just a huge collection of discrete points and actually I think it’s really a giant network with a changing pattern of connections between points where all that’s specified is how each point, each node is connected to others.”
From Stephen Wolfram’s 2003 H Paul Rockwood Memorial Lecture on “A New Kind of Science.”
A fundamental inverse square equation was derived directly from the underlying structure and is comparable to the three fundamental force equations of electricity, magnetism and gravitation. The bi-radial matrix is consistent and comparable with known physical interactions both structurally and mathematically. Properties of the matrix were introduced including invariance under spatial transformation which is consistent with conformal field theory and other proposed universal scaling mechanisms. Concurrent with the structural development definitions of space and time were advanced based on both practical observation and based on their being reciprocal aspects of motion. By developing the bi-radial matrix the geometric and numerical expression of this was shown to relate to the harmonic series and counting numbers. This is in pursuance to a quantum geometry based on "...combinatorial principles in terms of finite process such as counting or other basically simple manipulative procedures... ".
The BRM is revealing as a model of two interacting gravitational fields where the center of each mass are the respective "poles" of the combined field structure. This has similar properties to magnetism and electricity which both have opposite polarity. That a combined two body gravitational field , and electromagnetic fields have a bi-radial structure is supported by the current findings. Further the near harmonic structure of the BRM suggests relationships between the fundamental forces and harmonics. The bi-radial matrix provides a model of "force" expressed as a quantized harmonic interference pattern between to sets of quantum time potentials. It is useful as a model and coordinate system among several models including spin networks to aid in our understanding of space-time and fundamental forces.
The mathematical relationships emerge directly from the geometry suggesting fundamental relationships of which our current physical laws are special cases. By using a bi-radial coordinate system much of the attendant mathematics is simplified indicating the utility of the BRM in computational science.
Holographic Model of Universe
More Research and Development
There are additional parameters to the BRM including the "phase" which will be introduced regarding poles "A" and "B". This introduces rotation of the two poles "A" and "B" allowing the bi-radial matrix to model dynamic kinetic systems and to address in more detail non-locality and other phenomenon. An interactive visual demonstration is available at he link previously shown using the animation feature:
http://demonstrations.wolfram.com/BiradialMatrix/.
A further generalization and extension of the bi-radial matrix to describe N poles called the poly-radial matrix is under development. This allows detailed modelling of the N-body and many body problems including more detailed modelling of atomic structure. See diagram 36 below.
Much work needs to be done to fully develop the BRM and companion matrices in connection with physics. If this is to be a viable model on the atomic scale can it arrive at the various atomic spectra from first principles for instance? From the current presentation there are strong indications this is possible. To be a viable model on the macroscopic scale are there other predictions which result from the matrix along with the gravitational equilibrium zone prediction? As indicated before there is a companion matrix to the bi-radial matrix with inverse properties with regards to space and time.
This project opens up varied avenues of research and the brief survey given here only begins to suggest the direction this research can take. My personal interest relates to applications in energy research, unified field, computational science, the Lagrangian points, numerical methods and software applications in material science and education.
“ On a small enough scale space is just a huge collection of discrete points and actually I think it’s really a giant network with a changing pattern of connections between points where all that’s specified is how each point, each node is connected to others.”
From Stephen Wolfram’s 2003 H Paul Rockwood Memorial Lecture on “A New Kind of Science.”
A fundamental inverse square equation was derived directly from the underlying structure and is comparable to the three fundamental force equations of electricity, magnetism and gravitation. The bi-radial matrix is consistent and comparable with known physical interactions both structurally and mathematically. Properties of the matrix were introduced including invariance under spatial transformation which is consistent with conformal field theory and other proposed universal scaling mechanisms. Concurrent with the structural development definitions of space and time were advanced based on both practical observation and based on their being reciprocal aspects of motion. By developing the bi-radial matrix the geometric and numerical expression of this was shown to relate to the harmonic series and counting numbers. This is in pursuance to a quantum geometry based on "...combinatorial principles in terms of finite process such as counting or other basically simple manipulative procedures... ".
The BRM is revealing as a model of two interacting gravitational fields where the center of each mass are the respective "poles" of the combined field structure. This has similar properties to magnetism and electricity which both have opposite polarity. That a combined two body gravitational field , and electromagnetic fields have a bi-radial structure is supported by the current findings. Further the near harmonic structure of the BRM suggests relationships between the fundamental forces and harmonics. The bi-radial matrix provides a model of "force" expressed as a quantized harmonic interference pattern between to sets of quantum time potentials. It is useful as a model and coordinate system among several models including spin networks to aid in our understanding of space-time and fundamental forces.
The mathematical relationships emerge directly from the geometry suggesting fundamental relationships of which our current physical laws are special cases. By using a bi-radial coordinate system much of the attendant mathematics is simplified indicating the utility of the BRM in computational science.
Holographic Model of Universe
More Research and Development
There are additional parameters to the BRM including the "phase" which will be introduced regarding poles "A" and "B". This introduces rotation of the two poles "A" and "B" allowing the bi-radial matrix to model dynamic kinetic systems and to address in more detail non-locality and other phenomenon. An interactive visual demonstration is available at he link previously shown using the animation feature:
http://demonstrations.wolfram.com/BiradialMatrix/.
A further generalization and extension of the bi-radial matrix to describe N poles called the poly-radial matrix is under development. This allows detailed modelling of the N-body and many body problems including more detailed modelling of atomic structure. See diagram 36 below.
Much work needs to be done to fully develop the BRM and companion matrices in connection with physics. If this is to be a viable model on the atomic scale can it arrive at the various atomic spectra from first principles for instance? From the current presentation there are strong indications this is possible. To be a viable model on the macroscopic scale are there other predictions which result from the matrix along with the gravitational equilibrium zone prediction? As indicated before there is a companion matrix to the bi-radial matrix with inverse properties with regards to space and time.
This project opens up varied avenues of research and the brief survey given here only begins to suggest the direction this research can take. My personal interest relates to applications in energy research, unified field, computational science, the Lagrangian points, numerical methods and software applications in material science and education.
Diagram 36
Acknowledgements
Continuing gratitude and thanks to my long time friend and volunteer collaborator Bill Price for his broad contributions to this project including the original C++ program and help with the equations and proofs.Thanks to my friends at the Foundation For New Directions in Cambridge, MA for their support and creating opportunities for me to disseminate this work at their various work shops and informal discussion groups. Thanks to A. Michelle for assistance in graphic design. Thanks to the Wolfram Technical assistance team for help converting the original c++ code into Mathematica and enhancing the animation features.
