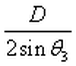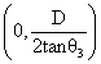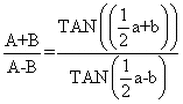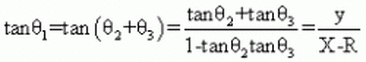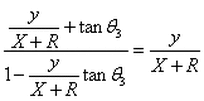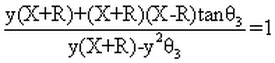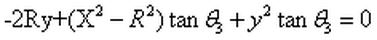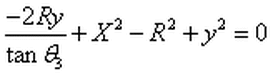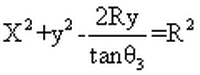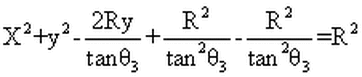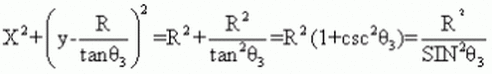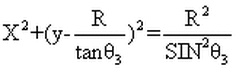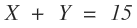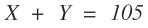PART 1 Equations and Proofs
Section 1 Shell Theorem
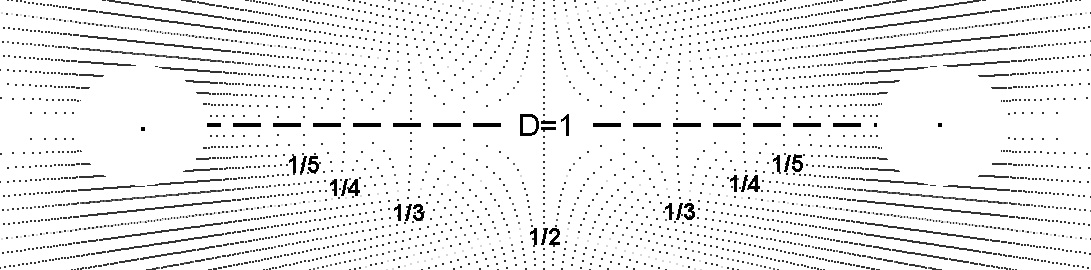
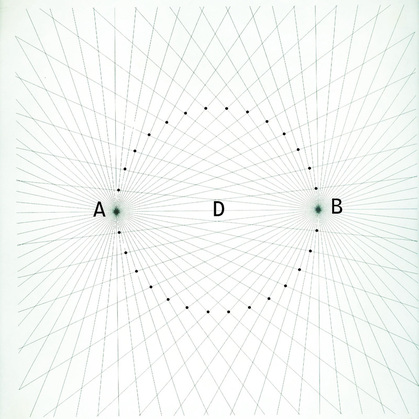
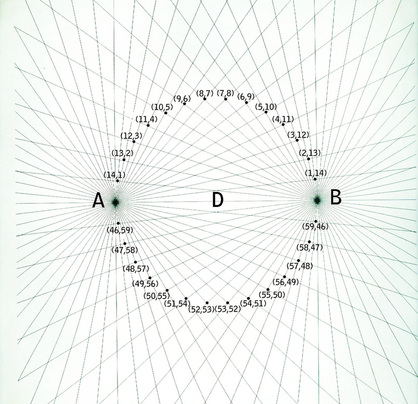
The shell theorem references the attraction lines in the bi-radial matrix as shown in the diagrams in the main page of this web site pertaining to the attraction lines of force.The vertices of these attraction lines fall on the paths of various non-concentric circles. The shell theorem facilitates the calculation of the radii of these circles and their center points.
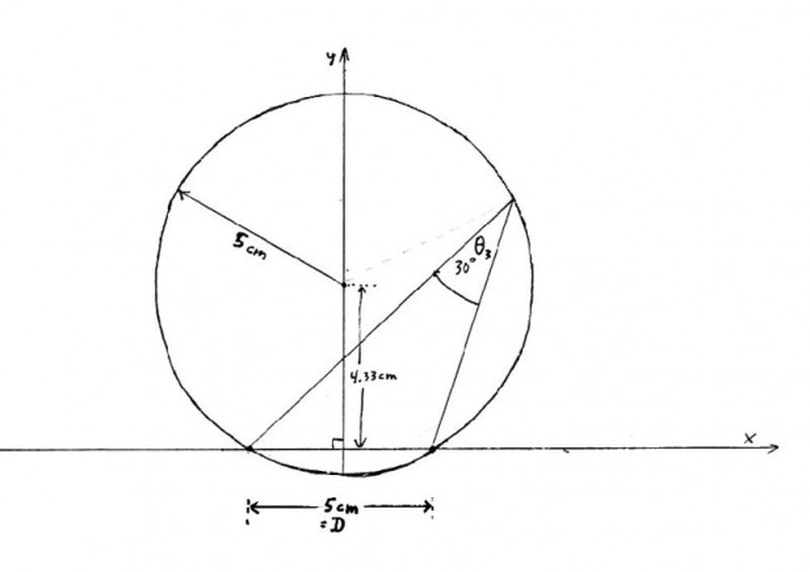
Shell Theorem: In the upper hemisphere of a bi-polar or bi-radial system (diagram 1) when two rays intersect at an included angle of θ3, the point of intersection will be located on a circle with radius:
and center at:
Section 2
Shell Theorem Diagram
Diagram 1
Section 3
Shell Theorem Proof
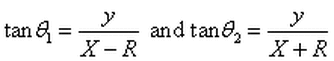
From the definition of tangent
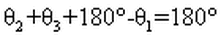
The sum of angles in a triangle must be 180 degrees.
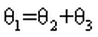
Hence
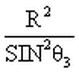
Formula for a circle radius
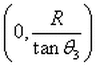
Center at:
PART 2
Section 1
Trapezoid formula
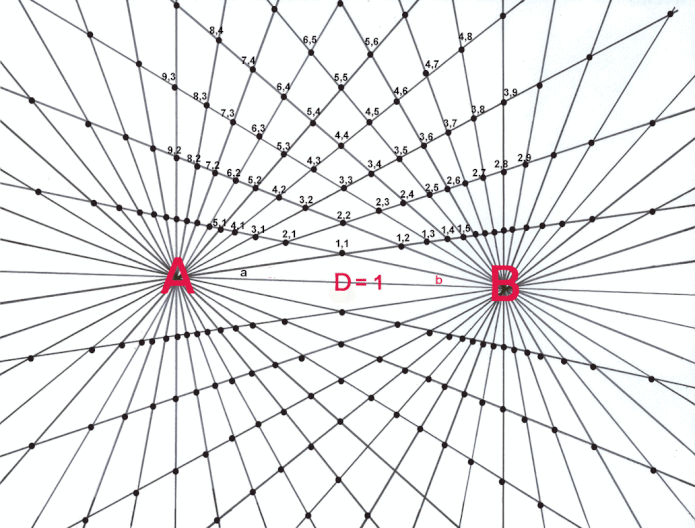Diagram 2
Here we will introduce a trapezoid formula based on the coordinates the BRM. In a subsequent presentation a trapezoid area formula based on the repulsion segments will be reviewed.
Given a trapezoid with an apex located at (X,Y) in a bi-radial matrix the area of the trapezoid is described in equation 1. The associated angles angles are shown in the diagrams below and their equations follow .
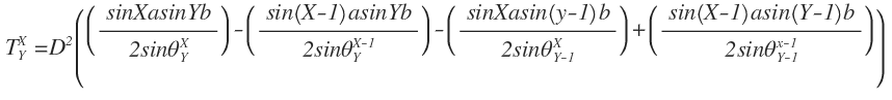Equation 1
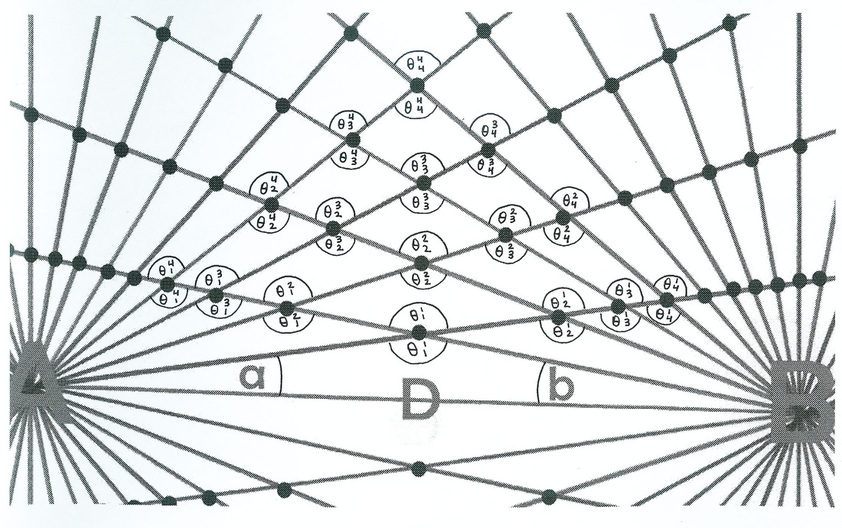Diagram 3
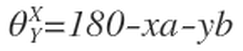Equation 2
From diagram 3 the equation for the apex angle theta is given by:
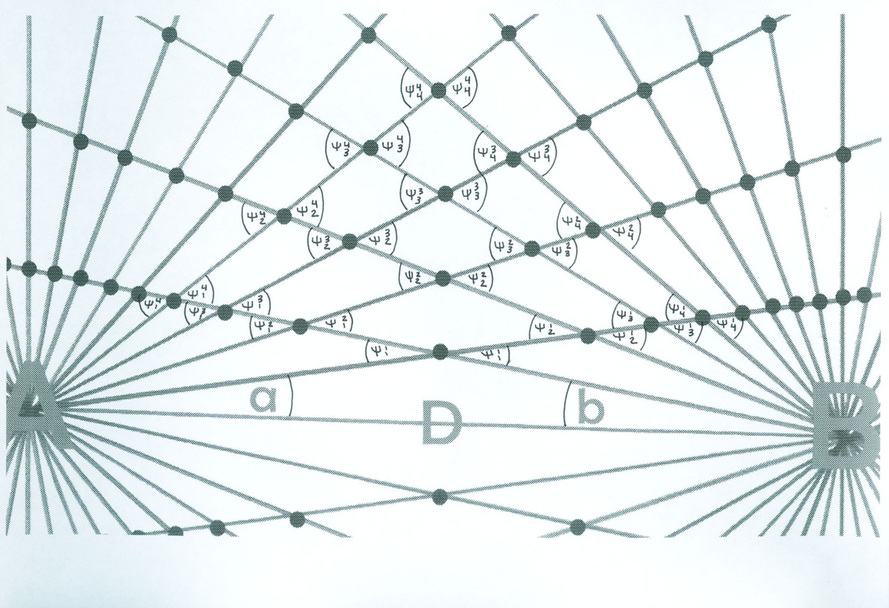Diagram 4
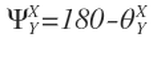Equation 3
The equation for the complimentary angles are given by:
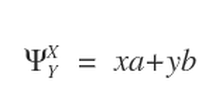Equation 4
PART 3
Conversion between Bi-radial and Cartesian coordinates
Section 1 Hyperbolas
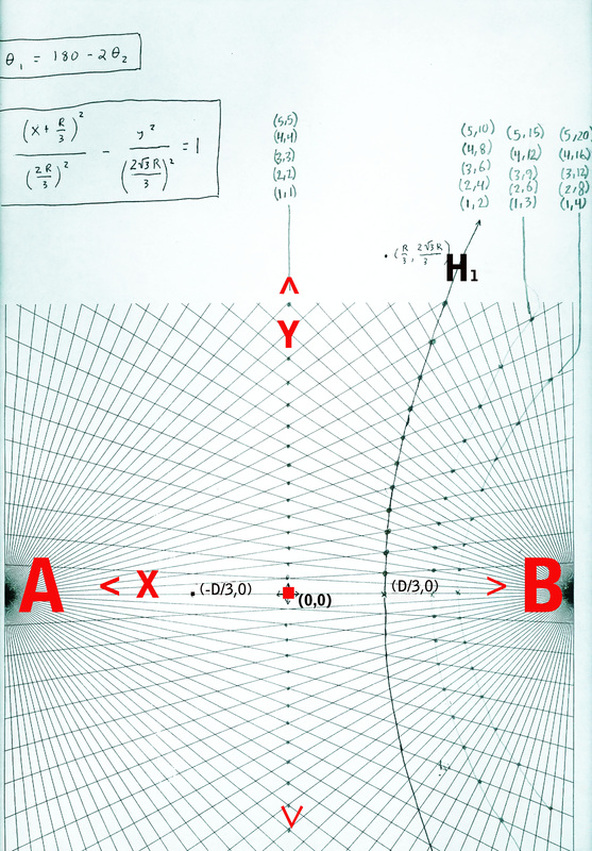Diagram 5
To convert from bi-radial coordinates to Cartesian coordinates the x,y origin of the Cartesian plain needs to be established within the bi-radial matrix.
In the spacial case bi-radial matrix where the number of rays from each pole A and B are equal the Cartesian x,y origin is located at the mid-point between A and B along the D segment.
The example in diagram 5 shows hyperbola H1. Equation 5 below represents the bi-radial equation for this curve and equation 6 is the Cartesian equivalent.
In the spacial case bi-radial matrix where the number of rays from each pole A and B are equal the Cartesian x,y origin is located at the mid-point between A and B along the D segment.
The example in diagram 5 shows hyperbola H1. Equation 5 below represents the bi-radial equation for this curve and equation 6 is the Cartesian equivalent.
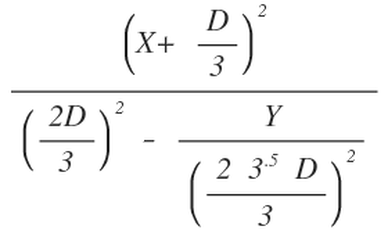Equation 5
Equation 5 is the Cartesian equation for the hyperbola H1 crossing the D segment at (D/3,0)
Equation 5
Equation 5
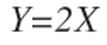Equation 6
Equation 6 is the bi-radial matrix based equation for same hyperbola H1 in diagram 5. By employing the bi-radial matrix the attendant mathematics is greatly simplified. This ability to simplify the mathematical description of conic sections clearly reveals the utility of the bi-radial matrix.
A general conversion formula between bi-radial and Cartesian coordinates can be derived.
A general conversion formula between bi-radial and Cartesian coordinates can be derived.
Section 2
Circles
Circles
A set of nodes in the bi-radial matrix where A=B=60 defining a circle is shown with the center located at the mid-point of the D segment. This is also a sub-set of the attraction lines shown in the main section.
|
Here the nodes are assigned their bi-radial coordinates. Using the present ray numbering system the equations for the circle in bi-radial coordinates are shown below. By using a different ray numbering convention the two equations can be reduced to a single equation.
|
Equation 1
|
Equation 2
|
Standard equation for a circle.
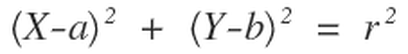Equation 3
Equation 3 is the standard equation for a circle who's center is located at (a,b) in a Cartesian coordinate system.
The bi-radial matrix is a higher dimensional coordinate system
Notice in both the case of the hyperbola and the circle the conventional Cartesian based math requires using the second power where as the bi-radial equations require only the first power. In the Cartesian coordinate system there is one (1) origin, a dimensionless point.
In the bi-radial matrix there are two (2) origins A and B separated by the D segment. This segment is one dimensional. Perhaps due to the fact that the bi-radial matrix represents a higher dimensional symmetry by a factor of 1 this allows the corresponding attendant mathematics to reduce the required exponents (which mathematically represent dimensions) by a factor of one.
In the bi-radial matrix there are two (2) origins A and B separated by the D segment. This segment is one dimensional. Perhaps due to the fact that the bi-radial matrix represents a higher dimensional symmetry by a factor of 1 this allows the corresponding attendant mathematics to reduce the required exponents (which mathematically represent dimensions) by a factor of one.
